题目内容
8.每个航班都有一个最早降落时间和最晚降落时间,在这个时间窗口内,飞机均有可能降落.甲航班降落的时间窗口为上午10点到11点,如果它准点降落时间为上午10点40分,那么甲航班晚点的概率是$\frac{1}{3}$;若甲乙两个航班在上午10点到11点之间共用一条跑道降落,如果两架飞机降落时间间隔不超过15分钟,则需要人工调度,在不考虑其他飞机起降的影响下,这两架飞机需要人工调度的概率是$\frac{7}{16}$.分析 利用几何概型,求出甲航班降落的时间窗口为上午10点到11点,如果它准点降落时间为上午10点40分,甲航班晚点的概率;试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,|x-y|≤$\frac{1}{4}$},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
解答  解:甲航班降落的时间窗口为上午10点到11点,如果它准点降落时间为上午10点40分,那么甲航班晚点的概率是$\frac{20}{60}$=$\frac{1}{3}$;
解:甲航班降落的时间窗口为上午10点到11点,如果它准点降落时间为上午10点40分,那么甲航班晚点的概率是$\frac{20}{60}$=$\frac{1}{3}$;
设甲乙两个航班到达的时间分别为(10+x)时、(10+y)时,
则0≤x≤1,0≤y≤1
若两架飞机降落时间间隔不超过15分钟,则|x-y|≤$\frac{1}{4}$
正方形的面积为1,落在两直线之间部分的面积为1-($\frac{3}{4}$)2=$\frac{7}{16}$,如图:
∴这两架飞机需要人工调度的概率是$\frac{7}{16}$.
故答案为$\frac{1}{3}$;$\frac{7}{16}$.
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
相关题目
18.等差数列{an}前n项和为Sn,公差d=-2,S3=21,则a1的值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 5 |
19.在三棱锥P-ABC中,D为底面ABC的边AB上一点,M为底面ABC内一点,且满足$\overrightarrow{AD}=\frac{3}{4}\overrightarrow{AB}$,$\overrightarrow{AM}=\overrightarrow{AD}+\frac{3}{5}\overrightarrow{BC}$,则三棱锥P-AMD与三棱锥P-ABC的体积比 $\frac{{{V_{P-AMD}}}}{{{V_{P-ABC}}}}$为( )
| A. | $\frac{9}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{9}{16}$ | D. | $\frac{9}{20}$ |
3.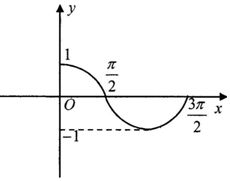 已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )
已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )
 已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )
已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )| A. | $f(x)=sin(x+\frac{π}{2})$ | B. | $f(x)=sin(x-\frac{π}{2})$ | C. | $f(x)=sin(2x+\frac{π}{2})$ | D. | $f(x)=sin(2x-\frac{π}{2})$ |
13.执行如图所示的程序框图,输出的k值为( )


| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
20. 如图是一个组合体的三视图,根据图中数据,可得该几何体的表面积(接触面积忽略不计)是( )
如图是一个组合体的三视图,根据图中数据,可得该几何体的表面积(接触面积忽略不计)是( )
 如图是一个组合体的三视图,根据图中数据,可得该几何体的表面积(接触面积忽略不计)是( )
如图是一个组合体的三视图,根据图中数据,可得该几何体的表面积(接触面积忽略不计)是( )| A. | 32π | B. | 36π | C. | 40π | D. | 48π |
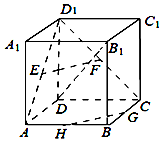 如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.
如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.