题目内容
16.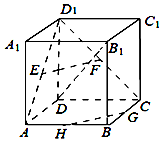 如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.
如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.(Ⅰ)求证:E,F,G,H四点共面;
(Ⅱ)求证:GH⊥B1D.
分析 (Ⅰ)连结AC,证明EF∥GH,即可证明E,F,G,H四点共面;
(Ⅱ)连结BD,证明GH⊥平面BDD1B1,即可证明GH⊥B1D.
解答 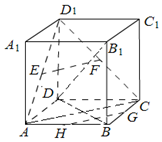 证明:(Ⅰ)如图,连结AC.(1分)
证明:(Ⅰ)如图,连结AC.(1分)
∵E,F分别是AD1、CD1的中点,∴EF∥AC.(2分)
∵G,H分别是BC、AB的中点,∴GH∥AC.(3分)
∴EF∥GH.(4分)
∴E,F,G,H四点共面.(5分)
(Ⅱ)连结BD.
∵ABCD-A1B1C1D1是正方体,∴AC⊥BD,AC⊥DD1.(7分)
∵BD∩DD1=D,BD,DD1?平面BDD1B1,∴AC⊥平面BDD1B1.(9分)
又∵GH∥AC,∴GH⊥平面BDD1B1,(10分)
又∵BD1?平面BDD1B1,∴GH⊥B1D.(11分)
点评 本题考查空间线线、线面位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表
由表中数据得回归直线方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中$\stackrel{∧}{b}$=-3,预测当气温为2℃时,用电量的度数是( )
| 气温(°C) | 20 | 16 | 12 | 4 |
| 用电量(度) | 14 | 28 | 44 | 62 |
| A. | 70 | B. | 68 | C. | 64 | D. | 62 |
4.“x-1>0”是“x2-1>0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.在复平面内,复数z=i(1+i),那么|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
6.函数f(x)=xm(1-x)n在区间[0,1]上的图象如图所示,则m,n的值为( )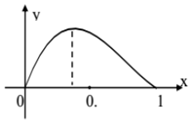

| A. | m=1,n=1 | B. | m=1,n=2 | C. | m=2,n=1 | D. | m=2,n=2 |
