题目内容
17.方程:22x+1-2x-3=0的解为$lo{g}_{2}\frac{3}{2}$.分析 令2x=t>0,方程即 2•t2-t-3=0,解得t,求得 x,从而得到方程22x+1-2x-3=0的解集.
解答 解:令2x=t>0,则方程 22x+1-2x-3=0即2•t2-t-3=0,解得t=$\frac{3}{2}$或t=-1(舍去),
即 2x=$\frac{3}{2}$,解得 x=$lo{g}_{2}\frac{3}{2}$.
故方程22x+1-2x-3=0的解集为{$lo{g}_{2}\frac{3}{2}$},
故答案为:$lo{g}_{2}\frac{3}{2}$.
点评 本题主要考查指数型函数的性质以及应用,求出2x的值,是解题的关键,属于中档题.

练习册系列答案
相关题目
12.已知在△ABC中,∠ACB=$\frac{π}{2}$,AB=2BC,现将△ABC绕BC所在直线旋转到△PBC,设二面角P-BC-A大小为θ,PB与平面ABC所成角为α,PC与平面PAB所成角为β,若0<θ<π,则( )
| A. | $α≤\frac{π}{3}$且$sinβ≤\frac{{\sqrt{3}}}{3}$ | B. | $α≤\frac{π}{3}$且$sinβ<\frac{{\sqrt{3}}}{3}$ | C. | $α≤\frac{π}{6}$且$β≥\frac{π}{3}$ | D. | $α≤\frac{π}{6}$且$β<\frac{π}{3}$ |
2.设x∈R,“x>1“的一个充分条件是( )
| A. | x>-1 | B. | x≥0 | C. | x≥1 | D. | x>2 |
9.函数y=sinx(cosx-sinx),x∈R的值域是( )
| A. | [-$\frac{1}{2}$,$\frac{3}{2}$] | B. | [$\frac{1-\sqrt{2}}{2},\frac{1+\sqrt{2}}{2}$] | C. | [-$\frac{3}{2},\frac{1}{2}$] | D. | [$\frac{-1-\sqrt{2}}{2},\frac{-1+\sqrt{2}}{2}$] |
6.函数f(x)=xm(1-x)n在区间[0,1]上的图象如图所示,则m,n的值为( )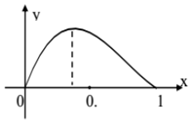

| A. | m=1,n=1 | B. | m=1,n=2 | C. | m=2,n=1 | D. | m=2,n=2 |
