题目内容
已知函数f(x)=3sin(ωx+
)的最小正周期为T且满足T∈(1,3),求ω的所有取值.
| 3 |
| π |
考点:三角函数的周期性及其求法
专题:计算题,三角函数的图像与性质
分析:先根据三角函数的最小正周期的求法求出最小正周期,再由T∈(1,3)确定k的范围,最后找出整数即可.
解答:
解:函数f(x)=3sin(ωx+
)的最小正周期为T=
∴1<
<3,
∴
<ω<2π
当ω为正整数时,ω的值为:3,4,5,6.
| 3 |
| π |
| 2π |
| ω |
∴1<
| 2π |
| ω |
∴
| 2π |
| 3 |
当ω为正整数时,ω的值为:3,4,5,6.
点评:本题主要考查三角函数的最小正周期的求法.高考对三角函数的考查以基础知识为主,平时要注意对于一些简单知识的积累和运用,属于基础题.

练习册系列答案
相关题目
若直线ax+(1-a)y=3与(a-1)x+(2a+3)y=2互相垂直,则a等于( )
| A、3 | ||
| B、1 | ||
C、0或-
| ||
| D、1或-3 |
若sinA=
,则sin(6π-A)的值为( )
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
定义在R上的函数f(x)满足:对任意α,β∈R,总有f(α+β)-[f(α)+f(β)]=2015,则下列说法正确的是( )
| A、f(x)+1是奇函数 |
| B、f(x)-1是奇函数 |
| C、f(x)+2015是奇函数 |
| D、f(x)-2015是奇函数 |
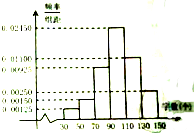 重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.
重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.