题目内容
已知抛物线y2=px(p>0)上的一点P(x0,1)到焦点的距离为
,x0为整数.
(1)求该抛物线的方程;
(2)求该抛物线到直线x-2y+4=0的距离的最小值.
| 5 |
| 4 |
(1)求该抛物线的方程;
(2)求该抛物线到直线x-2y+4=0的距离的最小值.
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得|PF|=
=
,且px0=1,从而
=
,由此能求出该抛物线的方程.
(2)设点坐标为(y2,y),将问题化为点到直线的距离L=
,由此能求出该抛物线到直线x-2y+4=0的距离的最小值.
(x0-
|
| 5 |
| 4 |
(
|
| 5 |
| 4 |
(2)设点坐标为(y2,y),将问题化为点到直线的距离L=
| |y2-2y+4| | ||
|
解答:
解:(1)∵抛物线y2=px(p>0)上的一点P(x0,1)到焦点的距离为
,x0为整数,
∴|PF|=
=
,且px0=1,即x0=
,
∴
=
,
由p>0,解得p=1,
∴该抛物线的方程为y2=x.
(2)∵由点在抛物线y2=x上,
∴设点坐标为(y2,y),将问题化为点到直线的距离:
L=
=
≥
.
∴该抛物线到直线x-2y+4=0的距离的最小值为
.
| 5 |
| 4 |
∴|PF|=
(x0-
|
| 5 |
| 4 |
| 1 |
| p |
∴
(
|
| 5 |
| 4 |
由p>0,解得p=1,
∴该抛物线的方程为y2=x.
(2)∵由点在抛物线y2=x上,
∴设点坐标为(y2,y),将问题化为点到直线的距离:
L=
| |y2-2y+4| | ||
|
=
| |(y-1)2+3| | ||
|
3
| ||
| 5 |
∴该抛物线到直线x-2y+4=0的距离的最小值为
3
| ||
| 5 |
点评:本题考查抛物线的方程的求法,考查抛物线到直线的距离的最小值的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
设等差数列{an}的前n项的和Sn,若a5-a3=4,a4+a6=-10,则当Sn取最小时,n等于( )
| A、6 | B、7 | C、8 | D、9 |
已知α,β是两个不同的平面,l,m,n是不同的直线,则正确命题为( )
| A、若l⊥m,l⊥n,m?α,n?α,则l⊥α |
| B、若l∥m,m?α,则l∥α |
| C、若α⊥β,α∩β=l,m?α,m⊥l,则m⊥β |
| D、若α⊥β,l⊥α,则l∥β |
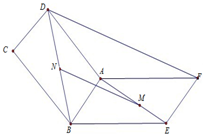 如图,已知ABCD与ABEF是两个平行四边形且不共面,M、N分别为AE、BD中点,求证:MN∥平面DAF.
如图,已知ABCD与ABEF是两个平行四边形且不共面,M、N分别为AE、BD中点,求证:MN∥平面DAF.