题目内容
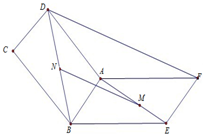如图，已知ABCD与ABEF是两个平行四边形且不共面，M、N分别为AE、BD中点，求证：MN∥平面DAF．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：通过线面平行的判定定理进行证明即可．
解答：
证明：如图示：
连接BF，
∵AE，BF都是平行四边形ABEF的对角线，且M是AE中点，
∴M是BF中点，
∵M，N分别为BF，BD中点，
∴MN∥DF，
∵MN?平面DAF，DF⊆平面DAF，
∴MN平行平面DAF．
连接BF，
∵AE，BF都是平行四边形ABEF的对角线，且M是AE中点，
∴M是BF中点，
∵M，N分别为BF，BD中点，
∴MN∥DF，
∵MN?平面DAF，DF⊆平面DAF，
∴MN平行平面DAF．
点评：本题考查了线面平行的判定定理，是一道基础题．
练习册系列答案
相关题目
设函数f（x）=
，若f（a）=8，则a=（ ）
|
| A、-8或-2 | B、-2或2 |
| C、-8或2 | D、-2或8 |
若复数z满足（1+i）z=i-2，则复数z对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合A={x| y=
}，B={y|y=x2-2x}，则A∩B=（ ）
| x2-4 |
| A、{y|-2≤y≤2} |
| B、{x|x≥-1} |
| C、{y|-1≤y≤2} |
| D、{x|x≥2} |
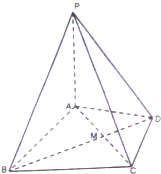如图，在四棱锥P-ABCD中，PA⊥面ABCD，△ABC是正三角形，AC△与BD的交点M恰好是AC的中点，又是PA=AB=2，∠CDA=120°．
