题目内容
已知α，β是两个不同的平面，l，m，n是不同的直线，则正确命题为（ ）
| A、若l⊥m，l⊥n，m?α，n?α，则l⊥α |
| B、若l∥m，m?α，则l∥α |
| C、若α⊥β，α∩β=l，m?α，m⊥l，则m⊥β |
| D、若α⊥β，l⊥α，则l∥β |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由线面位置关系，逐个选项验证可得．
解答：
解：A选项，当l⊥m，l⊥n，m?α，n?α时，需保证m和n相交时才有l⊥α，故A不正确；
B选项，若l∥m，m?α，则l∥α或l?α，故B不正确；
C选项，当α⊥β，α∩β=l，m?α，m⊥l，必有m⊥β，为平面与平面垂直的性质，故C正确；
D选项，当α⊥β，l⊥α，则l∥β或l?β，故D不正确．
故选：C
B选项，若l∥m，m?α，则l∥α或l?α，故B不正确；
C选项，当α⊥β，α∩β=l，m?α，m⊥l，必有m⊥β，为平面与平面垂直的性质，故C正确；
D选项，当α⊥β，l⊥α，则l∥β或l?β，故D不正确．
故选：C
点评：本题考查空间中的线面位置关系，属基础题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
若复数z满足（1+i）z=i-2，则复数z对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
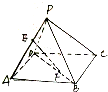如图，P是?ABCD所在平面外一点，E、F分别在PA、BD上，且PE：EA=BF：FD，求证：EF∥平面PBC．
