题目内容
2.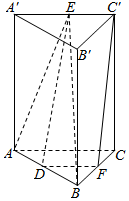 如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.
如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.(1)证明:C′F∥面ABE;
(2)证明:面ABE⊥面BB′C′C.
分析 (1)作AB中点D,连结DE、DF,推导出四边形EDFC′是平行四边形,由此能证明FC′∥面ABE.
(2)推导出BB′⊥AB,AB⊥BC,由此能证明面ABE⊥面BB′C′C.
解答 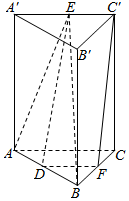 证明:(1)作AB中点D,连结DE、DF
证明:(1)作AB中点D,连结DE、DF
∵D、F分别为AB、BC的中点,∴DF$\underset{∥}{=}$$\frac{1}{2}$AC,
∵E为A′B′中点,∴EC′$\underset{∥}{=}$$\frac{1}{2}$AC,∴EC′$\underset{∥}{=}$DF,
∴四边形EDFC′是平行四边形,
∴DE∥FC′,又∵DE?平面ABE,FC′?面ABE,
∴FC′∥面ABE.
(2)∵直三棱柱ABC-A′B′C′中,BB′⊥平面ABC,AB?平面ABC,
∴BB′⊥AB,
∵侧面AA′C′C为正方形,且AA′=5,∴AC=5,
又∵AB=A′B′=3,BC=4,∴AC2=AB2+BC2,
即AB⊥BC,又∵BB′⊥AB,BB′∩BC=B,BB′、BC?面BB′C′C,
∴AB⊥面BB′C′C,又∵AB?面ABE,
∴面ABE⊥面BB′C′C.
点评 本题考查线面平行、面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
14.四位男生和两位女生排成一排,男生有且只有两位相邻,则不同排法的种数是( )
| A. | 72 | B. | 96 | C. | 144 | D. | 240 |
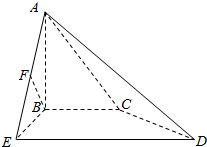 如图,四棱锥A-BCDE中,AB、BC、BE两两垂直且AB=BC=BE,DE∥BC,DE=2BC,F是AE的中点.
如图,四棱锥A-BCDE中,AB、BC、BE两两垂直且AB=BC=BE,DE∥BC,DE=2BC,F是AE的中点.