题目内容
10.在△ABC中,A,B,C的对边分别是a,b,c,且2acosB=2c-b.(Ⅰ)求A的大小;
(Ⅱ)若a=2,b+c=4,求△ABC的面积.
分析 (I)利用余弦定理即可得出;
(II)利用余弦定理可得bc,与b+c=4联立解出b,c,即可得出.
解答 解:(I)2acosB=2c-b,∴$2a×\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=2c-b,化为:b2+c2-a2=bc.
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
又A∈(0,π),
∴A=$\frac{π}{3}$.
(II)由余弦定理可得:a2=b2+c2-2bccosA,
∴22=(b+c)2-2bc-2bccosA=42-2bc(1+$\frac{1}{2}$),化为bc=4.
联立$\left\{\begin{array}{l}{b+c=4}\\{bc=4}\end{array}\right.$,解得b=c=2.
∴△ABC是等边三角形,
∴S△ABC=$\frac{\sqrt{3}}{4}$×22=$\sqrt{3}$.
点评 本题考查了余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.复数z在复平面内对应的点为A,点B与点A关于坐标原点对称,将点B向右平移一个单位,再向上平移一个单位,得到点C,若点C与点A对应复数表示的向量互相垂直且OA=OC,则复数z为( )
| A. | -1 | B. | 1或i | C. | i | D. | -i |
5.已知M={x|x=a2+2a+2,a∈N},N={y|y=b2-4b+5,b∈N},则M,N之间的关系是( )
| A. | M⊆N | B. | N⊆M | ||
| C. | M=N | D. | M与N之间没有包含关系 |
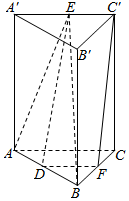 如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.
如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.