题目内容
12.若f(x)=x3-3x+m有且只有一个零点,则实数m的取值范围是(-∞,-2)∪(2,+∞).分析 求出f(x)的极值,令极大值小于零或极小值大于零即可.
解答 解:f′(x)=3x2-3,令f′(x)=0得x=±1.
当x<-1或x>1时,f′(x)>0,当-1<x<1时,f′(x)<0,
∴当x=-1时,f(x)取得极大值f(-1)=2+m,当x=1时,f(x)取得极小值f(1)=-2+m.
∵f(x)=x3-3x+m有且只有一个零点,
∴2+m<0或-2+m>0,解得m<-2或m>2.
故答案为(-∞,-2)∪(2,+∞).
点评 本题考查了函数的单调性与极值,函数的零点个数判断,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
3.若幂函数f(x)=xk在(0,+∞)上是减函数,则k可能是( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
7.已知三棱锥P-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,PC为球O的直径,该三棱锥的体积为$\frac{\sqrt{2}}{6}$,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
4.下列函数中,没有零点的是( )
| A. | f(x)=0 | B. | f(x)=2 | C. | f(x)=x2-1 | D. | f(x)=x-$\frac{1}{x}$ |
1.设f(x)为二次函数,且不等式f(x)>0之解为-2<x<4,则f(2x)<0之解为( )
| A. | -1<x<2 | B. | x<-1或x>2 | C. | x<-1或x>4 | D. | -4<x<8 | ||||
| E. | x<-4或x>8 |
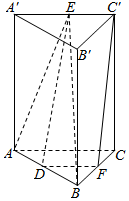 如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.
如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.