题目内容
12.已知数列{an}满足:$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$=$\frac{{n}^{2}}{2}$(n∈N*).(1)求数列{an}的通项公式;
(2)若bn=anan+1,Sn为数列{bn}的前n项和,对于任意的正整数n,Sn>2λ-$\frac{1}{3}$恒成立,求Sn及实数λ的取值范围.
分析 (1)利用递推关系即可得出an.
(2)利用“裂项求和”可得Sn,再利用数列的单调性与不等式的性质即可得出.
解答 解:(1)∵$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$=$\frac{{n}^{2}}{2}$(n∈N*),
∴当n=1时,$\frac{1}{{a}_{1}}$=$\frac{1}{2}$,解得a1=2.
当n≥2时,$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n-1}}$=$\frac{(n-1)^{2}}{2}$(n∈N*).
∴$\frac{1}{{a}_{n}}$=$\frac{{n}^{2}}{2}$-$\frac{(n-1)^{2}}{2}$,
解得an=$\frac{2}{2n-1}$,当n=1时也成立.
(2)bn=anan+1=$\frac{4}{(2n-1)(2n+1)}$=2$(\frac{1}{2n-1}-\frac{1}{2n+1})$.
∴数列{bn}的前n项和Sn=$2[(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$=2$(1-\frac{1}{2n+1})$,
∵对于任意的正整数n,Sn>2λ-$\frac{1}{3}$恒成立,
∴λ<$\frac{7}{6}$-$\frac{1}{2n+1}$.
∴λ<$\frac{5}{6}$.
∴实数λ的取值范围是$(-∞,\frac{5}{6})$.
点评 本题考查了递推关系、“裂项求和”、数列的单调性与不等式的性质,考查了推理能力与计算能力,属于中档题.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案| A. | 2i | B. | -2i | C. | -2 | D. | 2 |
| A. | -1 | B. | 1或i | C. | i | D. | -i |
| A. | y=x2+4 | B. | y=|tanx| | C. | y=cos2x | D. | y=3x-3-x |
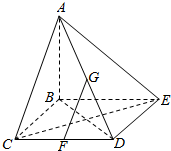 在四棱锥A-BCDE中,AB⊥平面BCDE,底面BCDE是正方形且AB=CD,点G,F分别是AD和CD的中点.求:
在四棱锥A-BCDE中,AB⊥平面BCDE,底面BCDE是正方形且AB=CD,点G,F分别是AD和CD的中点.求: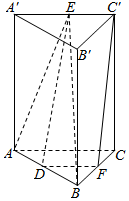 如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.
如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.