题目内容
17.已知S,A,B,C都是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=2,AB=3,BC=4,则球O的表面积等于29π.分析 由已知中S、A、B、C是球O表面上的点,SA⊥平面ABC,AB⊥BC,易S、A、B、C四点均为长宽高分别SA,AB,BC三边长的长方体的顶点,由长方体外接球的直径等于长方体对角线,可得球O的直径(半径),代入球的表面积公式即可得到答案.
解答 解:∵SA⊥平面ABC,AB⊥BC,
∴四面体S-ABC的外接球半径等于以长宽高分别SA,AB,BC三边长的长方体的外接球的半径
∵SA=2,AB=3,BC=4,
∴2R=$\sqrt{4+9+16}$=$\sqrt{29}$
∴球O的表面积S=4•πR2=29π
故答案为:29π.
点评 本题考查的知识点是球内接多面体,球的表面积公式,其中根据已知条件求出球O的直径(半径),是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列函数中,不是偶函数的是( )
| A. | y=x2+4 | B. | y=|tanx| | C. | y=cos2x | D. | y=3x-3-x |
5.已知M={x|x=a2+2a+2,a∈N},N={y|y=b2-4b+5,b∈N},则M,N之间的关系是( )
| A. | M⊆N | B. | N⊆M | ||
| C. | M=N | D. | M与N之间没有包含关系 |
12.已知复数z(1+i)=2i,则复数z=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
9.在复平面内,复数z=$\frac{2-i}{i}$的共轭复数$\overline{z}$对应的点所在的象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
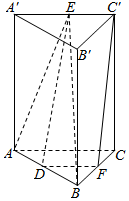 如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.
如图,在直三棱柱ABC-A′B′C′中,侧面AA′C′C为正方形,AA′=5,BC=4,A′B′=3,E、F分别是A′C′、BC的中点.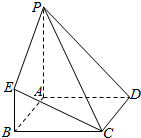 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=6,BE=3.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=6,BE=3.