题目内容
2014年春节联欢晚会结束后,某网站就观众最喜欢的节目类型进行调查.
(Ⅰ)网站记者从现场观看晚会的5名观众A,B,C,D,E中随机抽取2人进行访谈,求观众A恰好被抽中的概率;
(Ⅱ)该网站又通过网络从观看电视直播的观众中选取1000名进行调查,经数据处理后得下列图表:
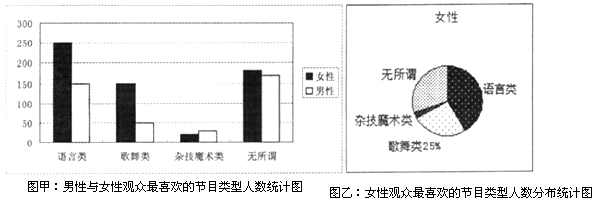
请你根据上述图表的数据信息,完成下列2×2列表的填写,并说明有多大的把握认为“是否最喜欢歌舞类节目和性别有关”
下面的临界值表及公式可供参考:
K2=
,其中n=a+b+c+d.
(Ⅰ)网站记者从现场观看晚会的5名观众A,B,C,D,E中随机抽取2人进行访谈,求观众A恰好被抽中的概率;
(Ⅱ)该网站又通过网络从观看电视直播的观众中选取1000名进行调查,经数据处理后得下列图表:

请你根据上述图表的数据信息,完成下列2×2列表的填写,并说明有多大的把握认为“是否最喜欢歌舞类节目和性别有关”
| 最喜欢歌舞类节目 | 不是最喜欢歌舞类节目 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 | 1000 |
| P(K2≥k) | 0.150 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:综合题,概率与统计
分析:(Ⅰ)确定基本事件的所有可能情况,即可求观众A恰好被抽中的概率;
(Ⅱ)根据图表可得2×2列表,计算K2,与临界值比较,即可得出结论.
(Ⅱ)根据图表可得2×2列表,计算K2,与临界值比较,即可得出结论.
解答:
解:(Ⅰ)5名观众A,B,C,D,E中随机抽取2人进行访谈,共有
=10种可能;观众A恰好被抽中,共有4种可能,故观众A恰好被抽中的概率为
=
;
(Ⅱ)2×2列表如下:
∴K2=
≈23.44>10.828,
∴有99%的把握认为“是否最喜欢歌舞类节目和性别有关.
| C | 2 5 |
| 4 |
| 10 |
| 2 |
| 5 |
(Ⅱ)2×2列表如下:
| 最喜欢歌舞类节目 | 不是最喜欢歌舞类节目 | 合计 | |
| 男 | 50 | 350 | 400 |
| 女 | 150 | 450 | 600 |
| 合计 | 200 | 800 | 1000 |
| 1000×(50×450-150×350)2 |
| 200×800×400×600 |
∴有99%的把握认为“是否最喜欢歌舞类节目和性别有关.
点评:本题考查概率的计算,考查2×2列表、独立性检验知识,考查学生的计算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
已知各项都是正数的等比数列{an}中,若a3是6a1与4a2的等差中项,则
=( )
| a4+a7 |
| a4+a5 |
| A、7 | ||
| B、9 | ||
C、
| ||
D、
|
 如图,E、F、G、H分别是任意四边形ABCD各边中点,若|
如图,E、F、G、H分别是任意四边形ABCD各边中点,若|| AB |
| BC |
| BA |
| AD |
| A、正方形 | B、梯形 | C、菱形 | D、矩形 |
已知tanα=-
,且α为第四象限角,则cosα等于( )
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
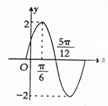 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<