题目内容
已知等差数列{an}中,a2+a3+a4+a5+a6=100,则a1+a7等于( )
| A、20 | B、30 | C、40 | D、50 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由题意和等差数列的性质可得a4=20,再由等差数列的性质可得a1+a7=2a4=40
解答:
解:由等差数列的性质可得a1+a7=a2+a6=a3+a5=2a4,
又a2+a3+a4+a5+a6=100,∴5a4=100,解得a4=20,
∴a1+a7=2a4=40
故选:C
又a2+a3+a4+a5+a6=100,∴5a4=100,解得a4=20,
∴a1+a7=2a4=40
故选:C
点评:本题考查等差数列的通项公式,涉及等差数列的性质,属基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
为了得到函数y=sin(3x+
)的图象,可以由函数y=sinx的图象( )
| π |
| 4 |
A、先向右平移
| ||||
B、先向左平移
| ||||
C、先将其横坐标缩短为原来的
| ||||
D、先将其横坐标缩短为原来的
|
已知函数f(x)=sin(ωx+
)(ω>0)的一条对称轴是x=
,则函数f(x)的最小正周期不可能是( )
| π |
| 4 |
| π |
| 8 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
复数(1-
)(1+i)=( )
| 1 |
| i |
| A、-2 | B、-2i | C、2 | D、2i |
已知集合A={1,2,3},B={2,3,4,5},则A∩B=( )
| A、{2,3} |
| B、{1,4,5} |
| C、{2,3,4} |
| D、{1,2,3,4,5} |
已知正方体ABCD-A1B1C1D1中,点O1为上底面A1C1的中心,若
=
+x
+y
,则x,y的值是( )
| AO1 |
| AA1 |
| AB |
| AD |
A、x=
| ||||
B、x=1,y=
| ||||
C、x=
| ||||
| D、x=1,y=1 |
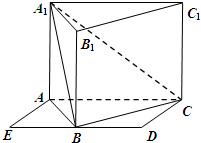 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AA1=4,∠E=60°,点B为DE中点,AB⊥BC.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AA1=4,∠E=60°,点B为DE中点,AB⊥BC.