题目内容
在等比数列{an}(q≠1)中,已知a1=1,a4=8.
(1)求{an}的通项公式;
(2)求Sn=a1+2a2+3a3+…+nan.
(1)求{an}的通项公式;
(2)求Sn=a1+2a2+3a3+…+nan.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)根据等比数列的通项公式,求出公比,即可求{an}的通项公式;
(2)利用错误相减法即可求Sn=a1+2a2+3a3+…+nan.
(2)利用错误相减法即可求Sn=a1+2a2+3a3+…+nan.
解答:
解:(1)在等比数列中,a4=q3=8,
解得q=2,则{an}的通项公式an=2n-1;
(2)∵an=2n-1,
∴nan=n•2n-1,
则Sn=a1+2a2+3a3+…+nan=1+2•21+3•22+…+n•2n-1,①
2Sn=2+2•22+3•23+…+n•2n,②
①一②得-Sn=1+2+22+23+…+•2n-1-n•2n=
-n•2n=2n-1-n•2n=(1-n)2n-1,
则Sn=(n-1)2n+1.
解得q=2,则{an}的通项公式an=2n-1;
(2)∵an=2n-1,
∴nan=n•2n-1,
则Sn=a1+2a2+3a3+…+nan=1+2•21+3•22+…+n•2n-1,①
2Sn=2+2•22+3•23+…+n•2n,②
①一②得-Sn=1+2+22+23+…+•2n-1-n•2n=
| 1-2n |
| 1-2 |
则Sn=(n-1)2n+1.
点评:本题主要考查等比数列的通项公式以及数列求和,要求熟练掌握求数列和的几种常见方法,错位相减法和裂项法,考查学生的运算能力.

练习册系列答案
相关题目
已知a>0,b>0,利用函数f(x)=3x+kx(k>0)的单调性,下列结论正确的是( )
| A、若3a+2a=3b+3b,则a>b |
| B、若3a+2a=3b+3b,则a<b |
| C、若2a-2a=2b-3b,则a>b |
| D、若2a-2a=2b-3b,则a<b |
已知x,y∈R,若lne-1i+2=y+xi,则x3+y=( )
| A、9 | B、3 | C、1 | D、2 |
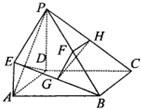 如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点. 在Rt△AOB中,
在Rt△AOB中,