题目内容
一份数学试卷由25个选择题构成，每个选择题有4个选项，其中有且仅有1个选项是正确的，每题选正确得4分，不选或选错得0分，满分100分．小强选对任一题的概率为0.8，则他在这次考试中得分的期望为（ ）
| A、60分 | B、70分 |
| C、80分 | D、90分 |
考点：离散型随机变量的期望与方差
专题：概率与统计
分析：设小强做对题数为ξ，则ξ～B（25，0.8），则他得分为4ξ，由此能求出结果．
解答：
解：设小强做对题数为ξ，
则ξ～B（25，0.8），
则他得分为4ξ，
E（4ξ）=4E（ξ）=4×25×0.8=80．
故选：C．
则ξ～B（25，0.8），
则他得分为4ξ，
E（4ξ）=4E（ξ）=4×25×0.8=80．
故选：C．
点评：本题考查离散型随机变量的数学期限，是中档题，解题时要注意二项分布的合理运用．
练习册系列答案
相关题目
计算：i（1+i）2=（ ）
| A、2i | B、-2i | C、2 | D、-2 |
若sin（α-
）=
，则cos（2α-
）的值是（ ）
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知x可以在区间[-t，4t]（t＞0）上任意取值，则x∈[-
t，t]的概率是（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在正方体ABCD-A1B1C1D1中，点M是棱BC的中点，则D1B与AM所成角的余弦值是（ ）
A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|
如图：四面体P-ABC为正四面体，M为PC的中点，则BM与AC所成的角的余弦值为（ ）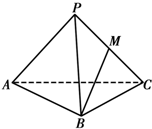 
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
已知直线l的方程为
x-y+
=0，则它的倾斜角为（ ）
| 3 |
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设实数a，b，c满足a+b+c=6，则a，b，c中（ ）
| A、至多有一个不大于2 |
| B、至少有一个不小于2 |
| C、至多有两个不小于2 |
| D、至少有两个不小于2 |
如图，梯形BCDE中，DE∥BC，CD⊥DE，ED=DC=