题目内容
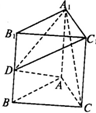 如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为( )
如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D,所以∠CEF或它的补角就是异面直线C1D与直线A1C所成的角,由此能求出异面直线C1D与直线A1C所成角的余弦值.
解答:
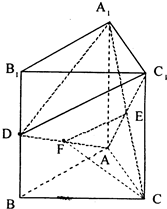 解:连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D,
解:连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D,
∴∠CEF或它的补角就是异面直线C1D与直线A1C所成的角,
∵AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又A1C1⊥A1B1,∴A1C1⊥平面A1B1BA∴AD⊥A1C1,AD⊥A1C1,则AD⊥AC,
又AF=
AD=
,
在△CEF中,CE=
A1C=
,EF=
C1D=
,CF=
=
,
cos∠CEF=
=
.
∴异面直线C1D与直线A1C所成角的余弦值为
.
故选:A.
 解:连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D,
解:连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D,∴∠CEF或它的补角就是异面直线C1D与直线A1C所成的角,
∵AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又A1C1⊥A1B1,∴A1C1⊥平面A1B1BA∴AD⊥A1C1,AD⊥A1C1,则AD⊥AC,
又AF=
| 1 |
| 2 |
| ||
| 2 |
在△CEF中,CE=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AC2+AF2 |
| ||
| 2 |
cos∠CEF=
| CE2+EF2-CF2 |
| 2CE•EF |
| ||
| 15 |
∴异面直线C1D与直线A1C所成角的余弦值为
| ||
| 15 |
故选:A.
点评:本题考查的知识点是异面直线及其所成的角,解法的关键是将异面直线夹角转化为解三角形问题,用余弦定理求解.

练习册系列答案
相关题目
若(
+
)n的展开式的二项式系数和为256,则展开式中含
的项的系数为( )
| x |
| 1 |
| x2 |
| 1 |
| x |
| A、8 | B、28 | C、56 | D、70 |
计算:i(1+i)2=( )
| A、2i | B、-2i | C、2 | D、-2 |
设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)-4f(-2)<0的解集为( )
| A、(-∞,-2012) |
| B、(-2012,0) |
| C、(-∞,-2016) |
| D、(-2016,-2014) |
已知正方形ABCD的边长为1,则|
+
|+|
-
|=( )
| AB |
| BC |
| AB |
| AD |
| A、4 | ||
| B、2 | ||
C、
| ||
D、2
|
已知函数f(x)=(2m-3)x2+5mx+7为偶函数,则函数f(x)在(1,4)是( )
| A、增函数 |
| B、减函数 |
| C、部分为增函数,部分为减函数 |
| D、无法确定增减性 |
如图:四面体P-ABC为正四面体,M为PC的中点,则BM与AC所成的角的余弦值为( ) 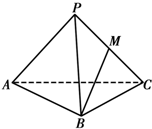

A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |