题目内容
若（3x-1）7=a7x7+a6x6+…+a1x+a0，则a7+a6+…+a1的值为（ ）
| A、1 | B、129 |
| C、128 | D、127 |
考点：二项式系数的性质
专题：二项式定理
分析：在所给的等式中，令x=0可得 a0=-1．再令x=1，可得a7+a6+…+a1+a0=27，从而求得a7+a6+…+a1 的值．
解答：
解：在（3x-1）7=a7x7+a6x6+…+a1x+a0中，令x=0，可得 a0=-1．
再令x=1，可得a7+a6+…+a1+a0=27，
∴a7+a6+…+a1 =27+1=129，
故选：B．
再令x=1，可得a7+a6+…+a1+a0=27，
∴a7+a6+…+a1 =27+1=129，
故选：B．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基题．
练习册系列答案
相关题目
若（
+
）n的展开式的二项式系数和为256，则展开式中含
的项的系数为（ ）
| x |
| 1 |
| x2 |
| 1 |
| x |
| A、8 | B、28 | C、56 | D、70 |
已知函数f（x）=（2m-3）x2+5mx+7为偶函数，则函数f（x）在（1，4）是（ ）
| A、增函数 |
| B、减函数 |
| C、部分为增函数，部分为减函数 |
| D、无法确定增减性 |
直线y-x+1=0的倾斜角为α，y轴上的截距为k，则（ ）
| A、α=135°，k=1 |
| B、α=45°，k=1 |
| C、α=45°，k=-1 |
| D、α=135°，k=-1 |
已知x可以在区间[-t，4t]（t＞0）上任意取值，则x∈[-
t，t]的概率是（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
棱长为1的正方体ABCD-A1B1C1D1中，点M，N分别在线段AB1，BC1上，且如图：四面体P-ABC为正四面体，M为PC的中点，则BM与AC所成的角的余弦值为（ ）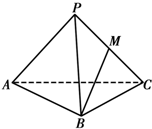 
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
圆x2+y2-2x+2y=0的圆心坐标为（ ）
| A、（1，-1） |
| B、（1，0） |
| C、（-1，-1） |
| D、（1，1） |