题目内容
一个圆柱的母线长度为2，底为半径为1的圆，则此圆柱的侧面积是（ ）
| A、π | B、2π | C、3π | D、4π |
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：圆柱侧面积=底面周长×高．由此利用题设条件能够求出结果．
解答：
解：圆柱沿一条母线剪开，所得到的侧面展开图是一个矩形，
它的长是底面圆的周长，即2π，宽为母线长为2，
所以它的面积4π．
故圆柱的侧面积为4π．
故选：D．
它的长是底面圆的周长，即2π，宽为母线长为2，
所以它的面积4π．
故圆柱的侧面积为4π．
故选：D．
点评：本题考查了圆柱的计算，掌握特殊立体图形的侧面展开图的特点，是解决此类问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知正方形ABCD的边长为1，则|
+
|+|
-
|=（ ）
| AB |
| BC |
| AB |
| AD |
| A、4 | ||
| B、2 | ||
C、
| ||
D、2
|
已知x可以在区间[-t，4t]（t＞0）上任意取值，则x∈[-
t，t]的概率是（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图：四面体P-ABC为正四面体，M为PC的中点，则BM与AC所成的角的余弦值为（ ）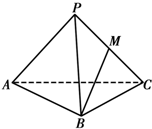 
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
已知直线l的方程为
x-y+
=0，则它的倾斜角为（ ）
| 3 |
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
圆x2+y2-2x+2y=0的圆心坐标为（ ）
| A、（1，-1） |
| B、（1，0） |
| C、（-1，-1） |
| D、（1，1） |
设实数a，b，c满足a+b+c=6，则a，b，c中（ ）
| A、至多有一个不大于2 |
| B、至少有一个不小于2 |
| C、至多有两个不小于2 |
| D、至少有两个不小于2 |