题目内容
若直线3x+(a+1)y-1=0与直线ax-2y+1=0互相垂直,则(-
+ax2)5展开式中x的系数为( )
| 1 |
| x |
| A、40 | B、-10 |
| C、10 | D、-40 |
考点:直线的一般式方程与直线的垂直关系,二项式系数的性质
专题:直线与圆
分析:由垂直关系可得a=2,代入要求的式子由二项式定理可得.
解答:
解:∵直线3x+(a+1)y-1=0与直线ax-2y+1=0互相垂直,
∴3a+(a+1)(-2)=0,解得a=2,
∴(-
+ax2)5=(-
+2x2)5,
∴展开式的通项Tr+1=
(-
)5-r(2x2)r
=(-1)5-r25
x3r-5,
令3r-5=1可得r=2,
∴(-
+ax2)5展开式中x的系数为:(-1)5-222
=-40,
故选:D.
∴3a+(a+1)(-2)=0,解得a=2,
∴(-
| 1 |
| x |
| 1 |
| x |
∴展开式的通项Tr+1=
| C | r 5 |
| 1 |
| x |
=(-1)5-r25
| C | r 5 |
令3r-5=1可得r=2,
∴(-
| 1 |
| x |
| C | 2 5 |
故选:D.
点评:本题考查直线的一般式的垂直关系,涉及二项式定理的应用,属基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知命题p:存在x∈R,使得x-10>lgx;命题q:对任意x∈R,都有x2>0,则( )
| A、命题“p或q”是假命题 |
| B、命题“p且q”是真命题 |
| C、命题“非q”是假命题 |
| D、命题“p且‘非q’”是真命题 |
已知f(x)是R上的偶函数,若将f(x)的图象向右平移一个单位,则得到一个奇函数的图象,若f(2)=-1,则f(1)+f(2)+f(3)+…+f(2014)=( )
| A、0 | B、1 |
| C、-1 | D、-1004.5 |
若a>b>0,则下列不等式中成立的是( )
A、
| ||||
| B、|a|<|b| | ||||
C、
| ||||
D、
|
设函数f(x)=|sin(2x+
)|,则下列关于函数f(x)的说法中正确的是( )
| π |
| 3 |
A、f(x)图象关于直线x=
| ||||
| B、f(x)的最小正周期为π | ||||
C、f(x)图象关于点(-
| ||||
D、f(x)在区间[
|
 已知a为如图所示的程序框图输出的结果,则二项式(a
已知a为如图所示的程序框图输出的结果,则二项式(a| x |
| 1 | ||
|
| A、-20 | ||
B、
| ||
| C、-192 | ||
| D、-160 |
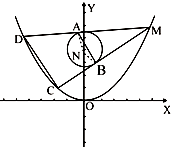 设抛物线E:x2=2y,圆N:x2+(y-4)2=1
设抛物线E:x2=2y,圆N:x2+(y-4)2=1