题目内容
下列命题错误的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1” |
| B、若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0 |
| C、△ABC中,sinA>sinB是A>B的充要条件 |
| D、若p∨q为真命题,则p、q均为真命题 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A,写出命题“若x2=1,则x=1”的否命题可判断A;
B,写出命题p:“?x0∈R,x02-x0+1≤0”的否定,可判断B;
C,△ABC中,利用正弦定理可判断sinA>sinB是A>B的充要条件,可判断C;
D,利用复合命题的真值表可判断D.
B,写出命题p:“?x0∈R,x02-x0+1≤0”的否定,可判断B;
C,△ABC中,利用正弦定理可判断sinA>sinB是A>B的充要条件,可判断C;
D,利用复合命题的真值表可判断D.
解答:
解:对于A,命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1”,故A正确;
对于B,若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0,故B正确
对于C,△ABC中,由正弦定理知sinA>sinB?a>b,在△ABC中,大边对大角,a>b?A>B,故sinA>sinB?A>B,sinA>sinB是A>B的充要条件,故C正确;
对于D,若p∨q为真命题,则p、q至少一个为真命题,故D错误
故选:D.
对于B,若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0,故B正确
对于C,△ABC中,由正弦定理知sinA>sinB?a>b,在△ABC中,大边对大角,a>b?A>B,故sinA>sinB?A>B,sinA>sinB是A>B的充要条件,故C正确;
对于D,若p∨q为真命题,则p、q至少一个为真命题,故D错误
故选:D.
点评:本题考查命题的真假判断与应用,着重考查四种命题之间的关系、全称命题与特称命题之间的关系、充分必要条件的概念及其真假判断,属于中档题.

练习册系列答案
相关题目
直线l:y=
x经过曲线C:y=
sinωx(ω>0)在区间[0,+∞)上的第一个最高点,则曲线C的最小正周期是( )
| 3 |
| 3 |
| A、4π | B、2π | C、4 | D、2 |
 如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.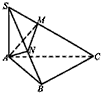 如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC.
如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC.