题目内容
已知a,b∈R,且a>b,则( )
| A、a2>b2 | ||||
B、
| ||||
| C、lg(a-b)>0 | ||||
D、(
|
考点:不等式的基本性质
专题:函数的性质及应用,不等式的解法及应用
分析:利用不等式的基本性质,可判断A,B,根据对数函数的图象和性质,可判断C,根据指数函数的图象和性质,可判断D.
解答:
解:当0>a>b时,a2<b2,故A不成立;
当a>0>b时,
<1,故B不成立;
当0<a-b<1时,lg(a-b)<0,故C不成立,
当a>b时,(
)a<(
)b恒成立,故D正确,
故选:D
当a>0>b时,
| a |
| b |
当0<a-b<1时,lg(a-b)<0,故C不成立,
当a>b时,(
| 1 |
| 2 |
| 1 |
| 2 |
故选:D
点评:本题考查的知识点是不等式的基本性质,指数函数的图象和性质,对数函数的图象和性质,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在正方体ABCD-A1B1C1D1中,下列各 式运算结果为向量
的是( )
①(
-
)-
;
②(
+
)-
;
③(
-
)-
;
④(
-
)+
.
| BD1 |
①(
| A1D1 |
| A1A |
| AB |
②(
| BC |
| BB1 |
| D1C1 |
③(
| AD |
| AB |
| DD1 |
④(
| B1D1 |
| A1A |
| DD1 |
| A、①② | B、②③ | C、③④ | D、①④ |
函数y=f(x)有f(x)=-f(x+1),且x∈[-1,1]时f(x)=1-x2.函数g(x)=
则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点个数为( )
|
| A、7 | B、8 | C、9 | D、10 |
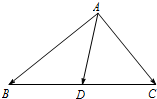 如图,点D是线段BC的中点,BC=6,且|
如图,点D是线段BC的中点,BC=6,且|| AB |
| AC |
| AB |
| AC |
| AD |
| A、6 | ||
B、2
| ||
| C、3 | ||
D、
|
函数f(x)=x+
+3在(-∞,0)上( )
| 4 |
| x |
| A、有最大值-1,无最小值 |
| B、无最大值,有最小值-1 |
| C、有最大值7,有最小值-1 |
| D、无最大值,有最小值7 |