题目内容
5.已知函数f(x)=2sin(2x+$\frac{2π}{3}$),若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).分析 根据y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:把函数f(x)=2sin(2x+$\frac{2π}{3}$)的图象向右平移$\frac{π}{6}$个单位长度得到的函数图象解析式为:
g(x)=f(x-$\frac{π}{6}$)=2sin[2(x-$\frac{π}{6}$)+$\frac{2π}{3}$]=2sin(2x+$\frac{π}{3}$).
故答案为:g(x)=2sin(2x+$\frac{π}{3}$).
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
15.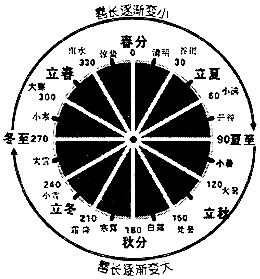 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 一丈二尺五寸 |
13.已知全集U=R,A={0,1,2,3},B={y|y=2x,x∈A},则(∁UA)∩B=( )
| A. | (-∞,0)∪(3,+∞) | B. | {x|x>3,x∈N} | C. | {4,8} | D. | [4,8] |
7.已知抛物线C:y2=4x的焦点为F,点A(0,-$\sqrt{3}$),若线段FA与抛物线C相交于点M,则|MF|=( )
| A. | $\frac{4}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
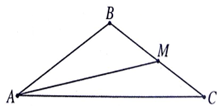 如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.
如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.