题目内容
13.已知全集U=R,A={0,1,2,3},B={y|y=2x,x∈A},则(∁UA)∩B=( )| A. | (-∞,0)∪(3,+∞) | B. | {x|x>3,x∈N} | C. | {4,8} | D. | [4,8] |
分析 根据全集U及A求出A的补集,找出A补集与B的交集即可.
解答 解:全集U=R,A={0,1,2,3},B={y|y=2x,x∈A}={1,2,4,8},
∴(∁UA)∩B={4,8},
故选:C
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
3.在△ABC中,内角A,B,C的对边分别为a,b,c,O是△ABC外接圆的圆心,若$\sqrt{2}αcosB=\sqrt{2}c-b$,且$\frac{cosB}{sinC}\overrightarrow{AB}+\frac{cosC}{sinB}\overrightarrow{AC}=m\overrightarrow{AO}$,则m的值是( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
18.已知双曲线$\frac{{x}^{2}}{3}$-y2=1的右焦点是抛物线y2=2px(p>0)的焦点,直线y=kx+m与抛物线交于A,B两个不同的点,点M(2,2)是AB的中点,则△OAB(O为坐标原点)的面积是( )
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2$\sqrt{3}$ |
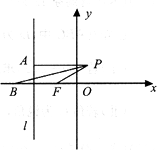 如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.
如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.