题目内容
7.已知抛物线C:y2=4x的焦点为F,点A(0,-$\sqrt{3}$),若线段FA与抛物线C相交于点M,则|MF|=( )| A. | $\frac{4}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 求出M的横坐标,利用三角形相似,即可得出结论.
解答 解:由题意,F(1,0),|AF|=2,设|MF|=d,则M到准线的距离为d,M的横坐标为d-1,
由三角形相似,可得$\frac{d-1}{1}=\frac{2-d}{2}$,∴d=$\frac{4}{3}$,
故选A.
点评 本题考查抛物线的方程与性质,考查三角形相似性质的运用,比较基础.

练习册系列答案
相关题目
6.矩形纸片ABCD中,AB=10cm,BC=8cm.将其按图(1)的方法分割,并按图(2)的方法焊接成扇形;按图(3)的方法将宽BC 2等分,把图(3)中的每个小矩形按图(1)分割并把4个小扇形焊接成一个大扇形;按图(4)的方法将宽BC 3等分,把图(4)中的每个小矩形按图(1)分割并把6个小扇形焊接成一个大扇形;…;依次将宽BC n等分,每个小矩形按图(1)分割并把2n个小扇形焊接成一个大扇形.当n→∞时,最后拼成的大扇形的圆心角的大小为( )
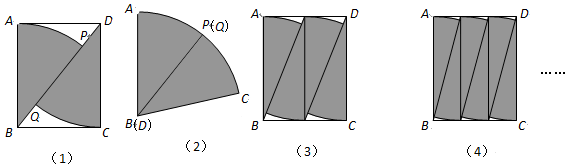

| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | C. | 大于$\frac{π}{2}$ | D. | 大于1.6 |
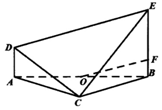 如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.
如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.