题目内容
16.已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,其上顶点B与左焦点F所在的直线的倾斜角为$\frac{π}{3}$,O为坐标原点OBF,三角形的周长为$3+\sqrt{3}$.(1)求椭圆E的方程;
(2)设椭圆E的右顶点为A,不过点A的直线l与椭圆E相交于P、Q两点,若以PQ为直径的圆经过点A,求证:直线l过定点,并求出该定点坐标.
分析 (1)由题意可得:$\frac{b}{c}$=tan$\frac{π}{3}$,a+b+c=3+$\sqrt{3}$,又a2=b2+c2,联立解出即可得出.
(2)A(2,0).设直线l的方程为:my+t=x,P(x1,y1),Q(x2,y2).与椭圆方程联立化为:(3m2+4)y2+6mty+3t2-12=0.以PQ为直径的圆经过点A,可得(x1-2)(x2-2)+y1y2=0,把根与系数的关系代入化简可得:t.即可得出.
解答 解:(1)由题意可得:$\frac{b}{c}$=tan$\frac{π}{3}$,a+b+c=3+$\sqrt{3}$,又a2=b2+c2,
联立解得:a=2,b=$\sqrt{3}$,c=1.
∴椭圆E的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
(2)证明:A(2,0).
设直线l的方程为:my+t=x,P(x1,y1),Q(x2,y2).
联立$\left\{\begin{array}{l}{my+t=x}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为:(3m2+4)y2+6mty+3t2-12=0,
∴y1+y2=$\frac{-6mt}{3{m}^{2}+4}$,y1•y2=$\frac{3{t}^{2}-12}{3{m}^{2}+4}$,(*)
∵以PQ为直径的圆经过点A,∴$\overrightarrow{AP}$⊥$\overrightarrow{AQ}$,
∴$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0,∴(x1-2)(x2-2)+y1y2=0,
即(my1+t-2)(my2+t-2)+y1y2=0,化为:(m2+1)y1y2+(mt-2m)(y1+y2)+(t-2)2=0,
把(*)代入可得:(m2+1)•$\frac{3{t}^{2}-12}{3{m}^{2}+4}$+(mt-2m)•$\frac{-6mt}{3{m}^{2}+4}$+(t-2)2=0,
化简可得:t=2或$\frac{2}{7}$.
t=2舍去.
代入直线l的方程:my+t=x,可得:my+$\frac{2}{7}$=x.
可得直线l经过定点:$(\frac{2}{7},0)$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、圆的性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.

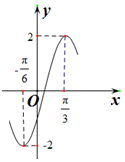 函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )
函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )| A. | $[\frac{π}{3},π]$和$[\frac{11π}{6},2π]$ | B. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{4π}{3},\frac{11π}{6}]$ | ||
| C. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{11π}{6},2π]$ | D. | $[\frac{π}{3},π]$和$[\frac{4π}{3},\frac{11π}{6}]$ |
| A. | M∩N=M | B. | M∪N=R | C. | M∩∁RN=φ | D. | ∁RM∪N=R |
| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | C. | 大于$\frac{π}{2}$ | D. | 大于1.6 |
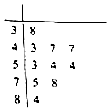 AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )
AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )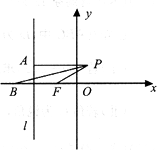 如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.
如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.