题目内容
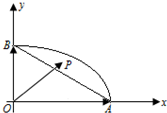 A,B是椭圆的右顶点及上顶点,由椭圆弧
A,B是椭圆的右顶点及上顶点,由椭圆弧| x2 |
| 4 |
| OP |
| OA |
| OB |
考点:向量在几何中的应用
专题:平面向量及应用
分析:先将A、B两点的坐标求出来,代入
=λ
+μ
,用μ、λ将P点坐标表示出来,再根据P在区域Ω内,构造出关于λ、μ的不等式组,化简后根据不等式的几何意义做出点M(λ,μ)的图象,再求其面积.
| OP |
| OA |
| OB |
解答:
解:由椭圆弧
+y2=1(x≥0,y≥0)得A(2,0),B(0,1),
∴直线AB方程为
+y=1,
且
=λ
+μ
=λ(2,0)+μ(0,1)=(2λ,μ),
又∵P是区域Ω上的任意一点(包括边界),
∴
,化简得
,
∴M点所在区域是由直线λ+μ=1,圆λ2+μ2=1,以及两坐标轴的正半轴围成的弓形部分,
∴S=
×12-
×1×1=
-
.
故答案为
-
.
| x2 |
| 4 |
∴直线AB方程为
| x |
| 2 |
且
| OP |
| OA |
| OB |
又∵P是区域Ω上的任意一点(包括边界),
∴
|
|
∴M点所在区域是由直线λ+μ=1,圆λ2+μ2=1,以及两坐标轴的正半轴围成的弓形部分,
∴S=
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
故答案为
| π |
| 4 |
| 1 |
| 2 |
点评:这是一个类似于“线性规划”的问题,思路是先根据题意找到点M(λ,μ)的横纵坐标所满足的条件,再结合其几何意义画出图象后,利用公式求出面积.

练习册系列答案
相关题目
设i为虚数单位,复数Z的共轭复数为
,且(
+1)(1-i)=2i,则复数Z的模为( )
. |
| Z |
. |
| Z |
A、
| ||
| B、5 | ||
| C、-2-i | ||
| D、1 |
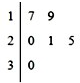 车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为
车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为