题目内容
已知
sin（x+40°）=cos（x+20°）+cos（x-20°），则tanx= ．
| 3 |
考点：两角和与差的余弦函数,三角函数的化简求值,两角和与差的正弦函数
专题：三角函数的求值
分析：由已知化简可得
sinxcos40°+
cosxsin40°=2cosxcos20°，变形可得tanx=
=
=
，展开化简可得．
| 3 |
| 3 |
| sinx |
| cosx |
2cos20°-
| ||
|
2cos(60°-40°)-
| ||
|
解答：
解：∵
sin（x+40°）=cos（x+20°）+cos（x-20°），
∴
sinxcos40°+
cosxsin40°
=cosxcos20°-sinxsin20°+cosxcos20°+sinxsin20°，
∴
sinxcos40°+
cosxsin40°=2cosxcos20°，
∴
sinxcos40°=2cosxcos20°-
cosxsin40°=（2cos20°-
sin40°）cosx，
∴tanx=
=
=
=
=
=
=
| 3 |
∴
| 3 |
| 3 |
=cosxcos20°-sinxsin20°+cosxcos20°+sinxsin20°，
∴
| 3 |
| 3 |
∴
| 3 |
| 3 |
| 3 |
∴tanx=
| sinx |
| cosx |
2cos20°-
| ||
|
2cos(60°-40°)-
| ||
|
=
cos40°+
| ||||
|
| cos40° | ||
|
| 1 | ||
|
| ||
| 3 |
点评：本题考查两角和与差的三角函数公式，正确变形是解决问题的关键，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
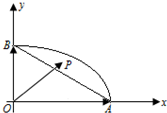A，B是椭圆的右顶点及上顶点，由椭圆弧