题目内容
已知函数f(x)的定义在R上的奇函数,当x>0时,f(x)=|x-a2|+|x-3a2|-4a2.若对任意x∈R,f(x)≤f(x+2),则实数a的取值范围为 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:通过对x与a的关系分类讨论,画出图象,路其周期性即可得出.
解答:
解:∵当x>0时,f(x)=|x-a2|+|x-3a2|-4a2.
∴当0<x≤a2时,f(x)=a2-x+3a2-x-4a2=-2x;
当a2<x≤3a2时,f(x)=x-a2+3a2-x-4a2=-2a2;
当x>3a2时,f(x)=x-a2+x-3a2-4a2=2x-8a2.
画出其图象如下:
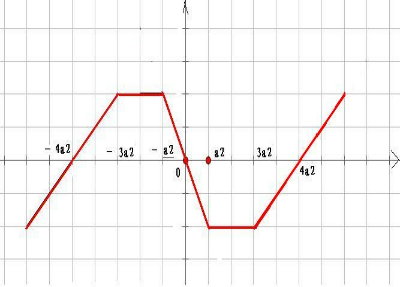
由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象,与x>0时的图象关于原点对称.
∵?x∈R,f(x+2)≥f(x),
∴8a2≤2,
解得a∈[-
,
].
∴当0<x≤a2时,f(x)=a2-x+3a2-x-4a2=-2x;
当a2<x≤3a2时,f(x)=x-a2+3a2-x-4a2=-2a2;
当x>3a2时,f(x)=x-a2+x-3a2-4a2=2x-8a2.
画出其图象如下:

由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象,与x>0时的图象关于原点对称.
∵?x∈R,f(x+2)≥f(x),
∴8a2≤2,
解得a∈[-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了函数的奇偶性、分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
已知函数f(x),对任意的x∈R,满足f(-x)+f(x)=0,f(2-x)=f(x),且当x∈[0,1]时,f(x)=ax,若方程f(x)-lgx=0恰有五个实根,则实数a的取值范围是( )
| A、(-lg11,-lg7)∪(2lg3,lg13) |
| B、(-2lg3,-lg7)∪(lg11,lg13) |
| C、(-lg13,-lg11)∪(lg7,2lg3) |
| D、(-lg13,-2lg3)∪(lg7,lg11) |
已知圆C:ρ=4sinθ与直线
(t为参数)交于A,B两点,则|AB|=( )
|
| A、2 | B、4 | C、6 | D、8 |
下列函数中,最小正周期为2π的是( )
| A、y=cosx |
| B、y=sin(2x+π) |
| C、y=tanx |
| D、y=|sinx| |
 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).确定x=
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).确定x=