题目内容
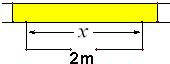
围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：元）．确定x=考点：解三角形的实际应用
专题：应用题,函数的性质及应用
分析：设矩形的另一边长为am，则根据围建的矩形场地的面积为360m2，易得a=
，此时再根据旧墙的维修费用为45元/m，新墙的造价为180元/m，我们即可得到修建围墙的总费用y表示成x的函数的解析式，利用基本不等式，我们易求出修建此矩形场地围墙的总费用最小值，及相应的x值．
| 360 |
| x |
解答：
解：设矩形的另一边长为a，
则y=45x+180（x-2）+180•2a=225x+360a-360．
由已知ax=360，得a=
，
所以 y=225x+
-360（x＞2）．
因为x＞0，所以225x+
≥2
=10800
所以y=225x+
-360≥10440，当且仅当225x=
时，等号成立．
解得当x=24m时，修建围墙的总费用最小，最小总费用是10440元．
故答案为：24．
解：设矩形的另一边长为a，则y=45x+180（x-2）+180•2a=225x+360a-360．
由已知ax=360，得a=
| 360 |
| x |
所以 y=225x+
| 3602 |
| x |
因为x＞0，所以225x+
| 3602 |
| x |
| 225×3602 |
所以y=225x+
| 3602 |
| x |
| 3602 |
| x |
解得当x=24m时，修建围墙的总费用最小，最小总费用是10440元．
故答案为：24．
点评：本题为函数的实际应用题，主要考查与函数有关的应用问题，利用条件建立函数关系是解决本题的关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
将直线y=
x绕原点顺时针旋转90°，再向左平移1个单位，所得到的直线的方程为（ ）
| 1 |
| 3 |
| A、y=-3x-3 |
| B、y=-3x+3 |
| C、y=-3x-1 |
| D、y=3x-3 |
在400毫升自来水中有一个大肠杆菌，今从中随机取出2毫升水样放到显微镜下观察，求发现大肠杆菌的概率为（ ）
| A、0.005 |
| B、0.004 |
| C、0.001 |
| D、0.002 |
