题目内容
已知函数f(x),对任意的x∈R,满足f(-x)+f(x)=0,f(2-x)=f(x),且当x∈[0,1]时,f(x)=ax,若方程f(x)-lgx=0恰有五个实根,则实数a的取值范围是( )
| A、(-lg11,-lg7)∪(2lg3,lg13) |
| B、(-2lg3,-lg7)∪(lg11,lg13) |
| C、(-lg13,-lg11)∪(lg7,2lg3) |
| D、(-lg13,-2lg3)∪(lg7,lg11) |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据条件得到函数f(x)的奇偶数,对称性和周期性,作出函数f(x)和y=lgx的图象,利用数形结合即可得到结论.
解答:
解:由f(-x)+f(x)=0得f(-x)=-f(x)则函数f(x)是奇函数,
由f(2-x)=f(x),则函数关于x=1对称,且f(2-x)=f(x)=-f(x-2),
则f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),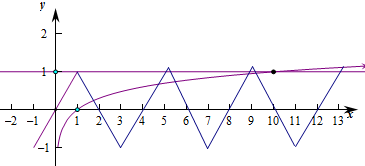
则函数f(x)的周期是4.
若方程f(x)-lgx=0恰有五个实根,
则等价为若方程f(x)=lgx恰有五个实根,即函数f(x)和y=lgx有5个交点,
∵当x∈[0,1]时,f(x)=ax
∴当x∈[-1,0]时,f(x)=-f(-x)=ax,即当x∈[-1,1]时,f(x)=ax,
作出函数f(x)和y=g(x)=lgx的图象如图:
若函数f(x)和y=lgx有5个交点,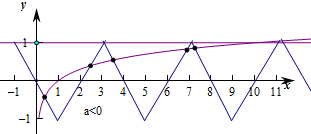
则当a>0时,则满足
,即
,
解得lg9<a<lg13,即2lg3<a<lg13,
若a<0,则满足
,即
,解得
,即-lg11<a<-lg7,
综上实数a的取值范围是(-lg11,-lg7)∪(2lg3,lg13),
故选:A
由f(2-x)=f(x),则函数关于x=1对称,且f(2-x)=f(x)=-f(x-2),
则f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),

则函数f(x)的周期是4.
若方程f(x)-lgx=0恰有五个实根,
则等价为若方程f(x)=lgx恰有五个实根,即函数f(x)和y=lgx有5个交点,
∵当x∈[0,1]时,f(x)=ax
∴当x∈[-1,0]时,f(x)=-f(-x)=ax,即当x∈[-1,1]时,f(x)=ax,
作出函数f(x)和y=g(x)=lgx的图象如图:
若函数f(x)和y=lgx有5个交点,

则当a>0时,则满足
|
|
解得lg9<a<lg13,即2lg3<a<lg13,
若a<0,则满足
|
|
|
综上实数a的取值范围是(-lg11,-lg7)∪(2lg3,lg13),
故选:A
点评:本题主要考查方程根的个数的应用,利用函数奇偶性和对称性以及周期性的性质,利用数形结合是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
已知全集U为实数集,设集合A={x|x2-4≤0},B={x|x≤0},A∩∁UB=( )
| A、[0,2] |
| B、(0,2] |
| C、(-∞,2] |
| D、[-2,0] |
在400毫升自来水中有一个大肠杆菌,今从中随机取出2毫升水样放到显微镜下观察,求发现大肠杆菌的概率为( )
| A、0.005 |
| B、0.004 |
| C、0.001 |
| D、0.002 |
若平面α⊥平面β,平面β⊥平面γ,则( )
| A、α∥γ |
| B、α⊥γ |
| C、α与γ相交但不垂直 |
| D、以上都有可能 |