题目内容
11.已知数列{an}的前n项和为Sn,Sn=$\frac{n^2}{2}+\frac{3n}{2}$,若数列{bn}满足bn=an+2-an+$\frac{1}{{{a_{n+2}}•{a_n}}}$,则数列{bn}的前n项和为Tn=$2n+\frac{5}{12}-\frac{2n+5}{2(n+2)(n+3)}$.分析 数列{an}的前n项和为Sn,Sn=$\frac{n^2}{2}+\frac{3n}{2}$,数列{an}是等差数列,a1=S1=2;2+a2=$\frac{{2}^{2}}{2}+\frac{3×2}{2}$,解得a2.an=n+1.可得bn=an+2-an+$\frac{1}{{{a_{n+2}}•{a_n}}}$=2+$\frac{1}{2}(\frac{1}{n+1}-\frac{1}{n+3})$,即可得出.
解答 解:∵数列{an}的前n项和为Sn,Sn=$\frac{n^2}{2}+\frac{3n}{2}$,
∴数列{an}是等差数列,a1=S1=2;2+a2=$\frac{{2}^{2}}{2}+\frac{3×2}{2}$=5,解得a2=3.
∴公差d=3-2=1.
∴an=2+(n-1)=n+1.
∴bn=an+2-an+$\frac{1}{{{a_{n+2}}•{a_n}}}$=n+3-(n+1)+$\frac{1}{(n+3)(n+1)}$=2+$\frac{1}{2}(\frac{1}{n+1}-\frac{1}{n+3})$,
则数列{bn}的前n项和为Tn=2n+$\frac{1}{2}$$[(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})$+$(\frac{1}{4}-\frac{1}{6})$+…+$(\frac{1}{n}-\frac{1}{n+2})+(\frac{1}{n+1}-\frac{1}{n+3})]$
=2n+$\frac{1}{2}$$(\frac{1}{2}+\frac{1}{3}-\frac{1}{n+2}-\frac{1}{n+3})$=$2n+\frac{5}{12}-\frac{2n+5}{2(n+2)(n+3)}$.
故答案为:$2n+\frac{5}{12}-\frac{2n+5}{2(n+2)(n+3)}$.
点评 本题考查了数列递推关系、等差数列的通项公式与求和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

| A. | 平面DD1C1C | B. | 平面A1DB | C. | 平面A1B1C1D1 | D. | 平面A1DB1 |
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |

| A. | k>4? | B. | k≤5? | C. | k>3? | D. | k≤4? |
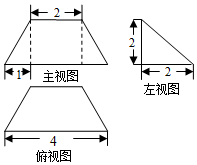
| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 12 |