题目内容
16.已知椭圆E的左、右焦点分别为F1,F2,过F1且斜率为2的直线交椭圆E于P,Q两点,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,则椭圆E的离心率为( )| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
分析 通过椭圆的定义可得丨PF2丨,丨PF1丨,利用勾股定理及离心率公式计算即得结论.
解答 解:由题可知:$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,则PF1⊥PF2,
由直线PQ的斜率k=2,则k=$\frac{丨P{F}_{2}丨}{丨P{F}_{1}丨}$=2,即丨PF2丨=2丨PF1丨,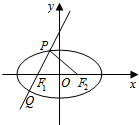
又椭圆的定义:丨PF2丨+丨PF1丨=2a,
∴丨PF1丨=$\frac{1}{3}$a,丨PF2丨=$\frac{4}{3}$a,
由勾股定理可知:(2c)2=($\frac{1}{3}$a)2+($\frac{4}{3}$a)2,
即:c2=$\frac{5}{9}$a2,
∴e=$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$,
故选A.
点评 本题考查求椭圆的离心率,涉及到三角函数的定义、勾股定理等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
7.“|x|+|y|≤1”是“x2+y2≤1”的( )条件.
| A. | 充分必要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
8.在等差数列{an}中,已知a3+a4=10,an-3+an-2=30,前n项之和是100,则项数n为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
5.下列说法中正确的是( )
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | “|a|>|b|”与“a2>b2”不等价. | |
| C. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0”. | |
| D. | 一个命题的否命题为真,则它的逆命题一定为真. |
6.已知正方体ABCD-A1B1C1D1,平面α过直线BD,α⊥平面AB1C,α∩平面AB1C=m,平面β过直线A1C1,β∥平面AB1C,β∩平面ADD1A1=n,则m,n所成角的余弦值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |