题目内容
1．某几何体的三视图如图所示，则该几何体的体积是（ ）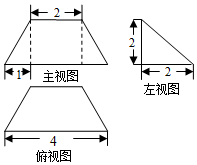
| A． | 4 | B． | $\frac{16}{3}$ | C． | $\frac{20}{3}$ | D． | 12 |
分析 由已知中的三视图可得：该几何体是两个三棱锥和一个棱柱组成的组合体，分别计算体积相加可得答案．
解答 解：由已知中的三视图可得：该几何体是两个三棱锥和一个棱柱组成的组合体，
底面面积S=$\frac{1}{2}$×2×2=2，
棱锥的高为1，棱柱的高为2，
故组合体的体积V=2×$\frac{1}{3}$×2×1+2×2=$\frac{16}{3}$，
故选：B
点评 本题考查的知识点是棱锥的体积和表面积，棱柱的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
12．化为推出一款6寸大屏手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下：
女性用户：
男性用户：
（1）如果评分不低于70分，就表示该用户对手机“认可”，否则就表示“不认可”，完成下列2×2列联表，并回答是否有95%的把握认为性别对手机的“认可”有关：
附：
K2=$\frac{n（a+d-b+c）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
（2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求2名用户中评分小于90分的概率．
女性用户：
| 分值区间 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P（K2≥k） | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
（2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求2名用户中评分小于90分的概率．
9．函数y=sin （2x+$\frac{π}{3}$）的图象可由函数y=cosx的图象（ ）
| A． | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍，再向左平移$\frac{π}{6}$个单位 | |
| B． | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍，再向右平移$\frac{π}{12}$个单位 | |
| C． | 先把各点的横坐标伸长到原来的2倍，再向左平移$\frac{π}{6}$个单位 | |
| D． | 先把各点的横坐标伸长到原来的2倍，再向右平移$\frac{π}{12}$个单位 |
如图，三棱柱ABC-DEF中，侧面ABED是边长为2的菱形，且∠ABE=$\frac{π}{3}$，BC=$\frac{\sqrt{21}}{2}$，点F在平面ABED内的正投影为G，且G在AE上，FG=$\sqrt{3}$，点M在线段CF上，且CM=$\frac{1}{4}$CF．
6．已知正方体ABCD-A1B1C1D1，平面α过直线BD，α⊥平面AB1C，α∩平面AB1C=m，平面β过直线A1C1，β∥平面AB1C，β∩平面ADD1A1=n，则m，n所成角的余弦值为（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
11．已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同，则图中的m，n的比值$\frac{n}{m}$=（ ）
| A． | 1 | B． | 3 | C． | $\frac{8}{3}$ | D． | $\frac{9}{2}$ |