题目内容
在极坐标系中，圆ρ=2cosθ的直角坐标方程为 ．
考点：简单曲线的极坐标方程
专题：选作题,坐标系和参数方程
分析：利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，将极坐标方程为ρ=2cosθ化成直角坐标方程．
解答：
解：∵圆ρ=2cosθ，
∴ρ2=2ρcosθ，
∵ρcosθ=x，ρsinθ=y，ρ2=x2+y2，
∴x2+y2-2x=0．
故答案为：x2+y2-2x=0．
∴ρ2=2ρcosθ，
∵ρcosθ=x，ρsinθ=y，ρ2=x2+y2，
∴x2+y2-2x=0．
故答案为：x2+y2-2x=0．
点评：本题考查点的极坐标和直角坐标的互化，属于基础题．
练习册系列答案
相关题目
等差数列{an}中a5+a6=4，则log2（2 a1•2 a2•2 a3•…•2a10）=（ ）
| A、10 |
| B、20 |
| C、40 |
| D、2+log25 |
若a=3sin60 °，b=log3cos60°，c=log3tan60°，则（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞b＞a |
| D、b＞a＞c |
已知全集U={1，2，3，4，5，6，7，8，9}，CU（A∪B）={1，3}，A∩（CUB）={2，4}，则集合B=（ ）
| A、{1，3，5，7，9} |
| B、{1，2，3，4} |
| C、{2，4，6，8} |
| D、{5，6，7，8，9} |
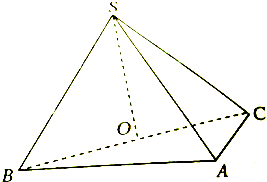如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC=90°，O为BC中点．
如图ABCD是菱形，PA⊥平面ABCD，E、F分别是PC、AB的中点．