题目内容
已知抛物线y2=8
x的焦点F与双曲线
-
=1（b＞0）的右焦点重合，求此双曲线的标准方程．
| 3 |
| x2 |
| 4 |
| y2 |
| b2 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线和抛物线的性质，求出焦点坐标，然后求出b2，即可得到双曲线的方程．
解答：
解：因为双曲线
-
=1（b＞0）的右焦点与抛物线y2=8
x的焦点重合，
而抛物线y2=8
x的焦点坐标为（2
，0），
∴c=2
，
∴4+b2=（2
）2
即b2=8，
∴双曲线方程为
-
=1．
| x2 |
| 4 |
| y2 |
| b2 |
| 3 |
而抛物线y2=8
| 3 |
| 3 |
∴c=2
| 3 |
∴4+b2=（2
| 3 |
即b2=8，
∴双曲线方程为
| x2 |
| 4 |
| y2 |
| 8 |
点评：本题考查抛物线和双曲线的方程和性质，考查运算能力，属于基础题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
设全集为实数集R，M={x|x2＞4}，N={x|1＜x≤3}，则图中阴影部分表示的集合是（ ）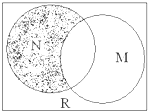 
| A、{x|1-2≤x＜1} |
| B、{x|-2≤x≤2} |
| C、{x|1＜x≤2} |
| D、{x|x＜2} |
集合A={x|y=ln（-x2+2x+3）}，B={y|y=ex}，则A∩B=（ ）
| A、{x|-1＜x＜0} |
| B、{x|0＜x＜3} |
| C、{x|x＞-1} |
| D、{x|x＜3} |
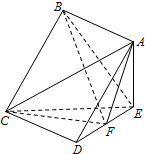如图，在四棱锥E-ABCD中，底面ABCD为正方形，AE⊥平面CDE，已知AE=DE=2，F为线段DE的中点．