题目内容

若a=3sin60  °，b=log3cos60°，c=log3tan60°，则（　　）
A、a＞b＞c
B、a＞c＞b
C、c＞b＞a
D、b＞a＞c
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用指数函数与对数函数、三角函数的单调性即可得出．
解答： 解：∵a=3sin60  °＞1，b=log3cos60°＜0，c=log3tan60°=
1
2
，
∴a＞c＞b．
故选：B．
点评：本题考查了指数函数与对数函数、三角函数的单调性，属于基础题．
练习册系列答案
相关题目
设m∈R，过定点A的动直线x+my=0与过定点B的动直线mx-y-m+3=0交于点P（x，y），则|PA|+|PB|的取值范围是
 
．
在空间直角坐标系中，A1是点A（-3，4，0）关于B（-1，2，3）的对称点，则|AA1|=（　　）
A、2
39
B、2
21
C、9
D、2
17
已知集合A={z||z|≤2，z∈C}，集合B={z|z=1+ai，a∈R}，其中C为复数集，i为虚数单位，若A∩B≠∅，则实数a的取值范围是（　　）
A、（-∞，-
3
）∪（
3
，+∞）
B、（-
3
，
3
）
C、（-∞，-
3
]∪[
3
，+∞）
D、[-
3
，
3
]
已知函数f（x）=
x2，(x＞0)
2，(x=0)
0，(x＜0)
则f（4）等于（　　）
A、16B、0C、2D、8
设全集为实数集R，M={x|x2＞4}，N={x|1＜x≤3}，则图中阴影部分表示的集合是（　　）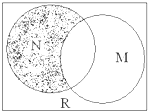 
A、{x|1-2≤x＜1}
B、{x|-2≤x≤2}
C、{x|1＜x≤2}
D、{x|x＜2}
命题“对任意的x∈R，x3-x2+1≤0”的否定是（　　）
A、存在x∉R，x∈R，x3-x2+1＞0
B、对任意的x∈R，x3-x2+1＞0
C、存在x∈R，x3-x2+1＞0
D、对任意的x∉R，x∈R，x3-x2+1＞0
在极坐标系中，圆ρ=2cosθ的直角坐标方程为
 
．
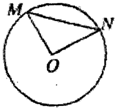如图，M是半径R的圆周上一个定点，在圆周上等可能的任取一点N，连接MN，则弦MN的长度超过
2
R的概率是（　　）
A、
1
5
B、
1
4
C、
1
3
D、
1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网