题目内容
下列命题真命题是（ ）
①?p∈{正数}，
为正数且
＜p； ②不存在实数x，使x＜4且x2+5x=24；
③?x∈R，使|x+1|≤1且x2＞4； ④对实数x，若x2-6x-7=0，则x2-6x-7≥0．
①?p∈{正数}，
| p |
| p |
③?x∈R，使|x+1|≤1且x2＞4； ④对实数x，若x2-6x-7=0，则x2-6x-7≥0．
| A、① | B、④ | C、②③ | D、①④ |
考点：命题的真假判断与应用
专题：简易逻辑
分析：①而0＜p≤1时，
≥p，即可判断出；
②当x=3＜4，x2+5x=24成立；
③由|x+1|≤1且x2＞4，解得x∈∅；
④对实数x，若x2-6x-7=0，则x2-6x-7≥0成立．
| p |
②当x=3＜4，x2+5x=24成立；
③由|x+1|≤1且x2＞4，解得x∈∅；
④对实数x，若x2-6x-7=0，则x2-6x-7≥0成立．
解答：
解：对于①?p∈{正数}，
为正数，只有p＞1时有
＜p，而0＜p≤1时，
≥p，因此不正确；
对于 ②当x=3＜4，x2+5x=24成立，因此不正确；
对于③由|x+1|≤1且x2＞4，解得x∈∅，因此不存在x∈R，使|x+1|≤1且x2＞4；
对于④对实数x，若x2-6x-7=0，则x2-6x-7≥0，成立．
综上可得：只有④是真命题．
故选：B．
| p |
| p |
| p |
对于 ②当x=3＜4，x2+5x=24成立，因此不正确；
对于③由|x+1|≤1且x2＞4，解得x∈∅，因此不存在x∈R，使|x+1|≤1且x2＞4；
对于④对实数x，若x2-6x-7=0，则x2-6x-7≥0，成立．
综上可得：只有④是真命题．
故选：B．
点评：本题考查了简易逻辑的判定，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
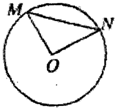如图，M是半径R的圆周上一个定点，在圆周上等可能的任取一点N，连接MN，则弦MN的长度超过| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|