题目内容
14.定义域为[a,b]的函数f(x)的图象的左、右端点分别为A、B,点M(x,y)是f(x)的图象上的任意一点,且x=λa+(1-λ)b(λ∈R).向量$\overrightarrow{ON}=λ\overrightarrow{OA}+(1-λ)\overrightarrow{OB}$,其中O为坐标原点.若|$\overrightarrow{MN}$|≤k恒成立,则称函数f(x)在[a,b]上“k阶线性相似”.若函数y=x2-3x+2在[1,3]上“k阶线性相似”,则实数k的取值范围为( )| A. | [0,+∞] | B. | [1,+∞] | C. | [$\frac{3}{2}$,+∞] | D. | [$\frac{1}{2}$,+∞) |
分析 根据条件可以得到M,N点的横坐标相同,且点N在直线AB上,而可以求出A,B两点的坐标,从而可以得到直线AB的方程为y=x-1,这样即可得出$|\overrightarrow{MN}|=|{x}^{2}-4x+3|$.而根据x的范围即可求出$|\overrightarrow{MN}|$的范围,即得出$|\overrightarrow{MN}|$的最大值,从而便可得出实数k的取值范围.
解答 解:由题意,M,N点的横坐标相同,$|\overrightarrow{MN}|≤k$,即$|\overrightarrow{MN}{|}_{max}≤k$;
∵A(1,0),B(3,2);
∴直线AB的方程为y=x-1;
根据题意知,点N在直线AB上;
∴$|\overrightarrow{MN}|=|{x}^{2}-3x+2-x+1|=|{x}^{2}-4x+3|$;
∵x∈[1,3],x2-4x+3=0的两根为1,3;
∴|x2-4x+3|∈[0,1];
∴$|\overrightarrow{MN}{|}_{max}=1$;
∴1≤k;
∴实数k的取值范围为[1,+∞).
故选:B.
点评 考查向量坐标的加法和数乘运算,理解“k阶线性相似”的概念,由$\overrightarrow{ON}=λ\overrightarrow{OA}+(1-λ)\overrightarrow{OB}$知N,A,B三点共线,横坐标相同的两点距离的求法,要熟悉二次函数的图象.

练习册系列答案
相关题目
5.如图是函数f(x)=sin(x+φ)一个周期内的图象,则φ可能等于( )
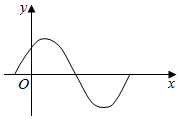

| A. | $\frac{5π}{6}$ | B. | $\frac{π}{2}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
2.若质点A按规律s=2t2运动,则质点A在t=1时的瞬时速度是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{4}$ | D. | 4 |
19.在梯形ABCD中AD∥BC,已知AD=4,BC=6,若$\overrightarrow{CD}$=m$\overrightarrow{BA}$+n$\overrightarrow{BC}$(m,n∈R)则$\frac{m}{n}$=( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
3.由曲线y=x3,直线x=0,x=1及y=0所围成的曲边梯形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
4.有算法语句如下,其运算的结果是( )


| A. | 12 | B. | 3 | C. | 4 | D. | $\frac{275}{72}$ |