题目内容
9.已知函数y=x3+px2+qx,其图象与x轴切于非原点的一点,且该函数的极小值是-4,那么切点坐标为(-3,0).分析 设切点(a,0)(a≠0),f(x)=x(x2+px+q).由题意得:方程x2+px+q=0有两个相等实根a,故可得f(x)=x(x-a)2=x3-2ax2+a2x,再利用y极小值=-4,可求a=-3,从而得到切点.
解答 解:设切点(a,0)(a≠0),
f(x)=x(x2+px+q),
由题意得:方程x2+px+q=0有两个相等实根a,
故可得f(x)=x(x-a)2=x3-2ax2+a2x
f′(x)=3x2-4ax+a2=(x-a)(3x-a),
令f′(x)=0,则x=a或$\frac{a}{3}$,
∵f(a)=0≠-4,
∴f($\frac{a}{3}$)=-4,
于是$\frac{a}{3}$($\frac{a}{3}$-a)2=-4,
∴a=-3,
即有切点为(-3,0),
故答案为:(-3,0).
点评 本题以函数为载体,考查函数的极值,考查导数的几何意义,属于中档题.

练习册系列答案
相关题目
19.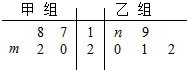 某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
 某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )| A. | m=3,n=8 | B. | m=4,n=7 | C. | m=5,n=6 | D. | m=6,n=5 |
20.已知A、B、C是平面上不共线的三点,O是△ABC的重心(三条中线的交点),AB边的中点为D.动点P满足$\overrightarrow{OP}=\frac{1}{3}(\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+2\overrightarrow{OC})$,则点P一定为△ABC的( )
| A. | 线段CD的中点 | B. | 线段CD靠近C的四等分点 | ||
| C. | 重心 | D. | 线段CD靠近C的三等分点 |
4.在△ABC中,若$A=\frac{π}{6},a=2,b=2\sqrt{3}$,则B=( )
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{2π}{3}$ |
14.定义域为[a,b]的函数f(x)的图象的左、右端点分别为A、B,点M(x,y)是f(x)的图象上的任意一点,且x=λa+(1-λ)b(λ∈R).向量$\overrightarrow{ON}=λ\overrightarrow{OA}+(1-λ)\overrightarrow{OB}$,其中O为坐标原点.若|$\overrightarrow{MN}$|≤k恒成立,则称函数f(x)在[a,b]上“k阶线性相似”.若函数y=x2-3x+2在[1,3]上“k阶线性相似”,则实数k的取值范围为( )
| A. | [0,+∞] | B. | [1,+∞] | C. | [$\frac{3}{2}$,+∞] | D. | [$\frac{1}{2}$,+∞) |
19.设α为锐角,且lg(1-cosα)=m,lg(1+cosα)=n,则lgsinα=( )
| A. | m-n | B. | m+n | C. | $\frac{1}{2}$(m-n) | D. | $\frac{1}{2}$(m+n) |