题目内容
4.已知:平面上两个不相等向量,$\overrightarrow{m}$=(3,4),$\overrightarrow{n}$=(x+1,2x)(1)若($\overrightarrow{m}$+$\overrightarrow{n}$)⊥($\overrightarrow{m}$-$\overrightarrow{n}$),求实数x;
(2)若$\overrightarrow{m}$•$\overrightarrow{n}$=14,求$\overrightarrow{m}$与$\overrightarrow{n}$的夹角的余弦值.
分析 (1)根据向量的垂直的条件得到关于x的方程,解得即可,
(2)先根据向量的数量积求出x的值,再根据向量的夹角公式即可求出.
解答 解:(1)∵$\overrightarrow{m}$=(3,4),$\overrightarrow{n}$=(x+1,2x),($\overrightarrow{m}$+$\overrightarrow{n}$)⊥($\overrightarrow{m}$-$\overrightarrow{n}$),
∴($\overrightarrow{m}$+$\overrightarrow{n}$)•($\overrightarrow{m}$-$\overrightarrow{n}$)=$\overrightarrow{m}$2-$\overrightarrow{n}$2=32+42-(x+1)2--4x2=0,
∴x=-$\frac{12}{5}$或x=2,
(2)∵$\overrightarrow{m}$•$\overrightarrow{n}$=14,
∴3(x+1)+4×2x=14,
∴x=1,
∴$\overrightarrow{n}$=(2,2),
∴|$\overrightarrow{n}$|=2$\sqrt{2}$,|$\overrightarrow{m}$|=5,
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{14}{2\sqrt{2}×5}$=$\frac{7\sqrt{2}}{10}$.
点评 本题考查了向量垂直的条件以及向量的夹角公式,属于基础题.

 阅读快车系列答案
阅读快车系列答案| A. | 0 | B. | 2tanθ | C. | -2tanθ | D. | $\frac{1}{2tanθ}$ |
| A. | 90° | B. | 60° | C. | 135° | D. | 150° |
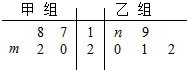 某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )| A. | m=3,n=8 | B. | m=4,n=7 | C. | m=5,n=6 | D. | m=6,n=5 |
| A. | a⊥b,a⊥c,b?α,c?α | B. | a∥b,b⊥α | C. | a∩b=A,b?α,a⊥b | D. | a⊥b,b∥α |
| A. | 0 | B. | -2 | C. | -4 | D. | 2 |
| A. | [0,+∞] | B. | [1,+∞] | C. | [$\frac{3}{2}$,+∞] | D. | [$\frac{1}{2}$,+∞) |