题目内容
已知函数f(x),对任意x∈R,有f(x-2)=
f(x),当x∈[0,2]时,f(x)=1-(x-1)2.
①若函数g(x)=lnx,则函数h(x)=f(x)-g(x)的区间(0,4]上有3个零点;
②若函数g(x)=
,函数h(x)=g(x)+ax有2个零点,则a>0或a<-
;
③若函数h(x)=f(x)-a在区间(-2,4)有4个零点,则a范围是(
,1);
④若函数g(x)=
-a有3个零点,则a的范围是(
,
)∪(0,12-8
);
以上正确的命题有 (写出所有正确的序号).
| 1 |
| 2 |
①若函数g(x)=lnx,则函数h(x)=f(x)-g(x)的区间(0,4]上有3个零点;
②若函数g(x)=
|
| 2 |
| 3 |
③若函数h(x)=f(x)-a在区间(-2,4)有4个零点,则a范围是(
| 1 |
| 2 |
④若函数g(x)=
| f(x) |
| x |
-3+2
| ||
| 2 |
-5+
| ||
| 4 |
| 2 |
以上正确的命题有
考点:抽象函数及其应用
专题:计算题,数形结合,函数的性质及应用
分析:作出y=lnx和y=f(x)(0<x<4)的图象,观察有3个交点,即可判断①;
画出y=f(x)(0≤x≤4)和y=|2x-1|(x<0)的图象,以及直线y=-ax,讨论a>0的交点情况,即可判断②;
画出y=a和y=f(x)在(-2,4)的图象,通过图象观察得到4个零点时a的范围,即可判断③;
画出y=f(x)和直线y=ax的图象,通过图象观察,当x>0时,由于f(x)不存在最大值,故不可能有三个交点即可判断④.
画出y=f(x)(0≤x≤4)和y=|2x-1|(x<0)的图象,以及直线y=-ax,讨论a>0的交点情况,即可判断②;
画出y=a和y=f(x)在(-2,4)的图象,通过图象观察得到4个零点时a的范围,即可判断③;
画出y=f(x)和直线y=ax的图象,通过图象观察,当x>0时,由于f(x)不存在最大值,故不可能有三个交点即可判断④.
解答:
 解:对于①,当2<x≤4时,0<x-2≤2,
解:对于①,当2<x≤4时,0<x-2≤2,
f(x-2)=1-(x-3)2=
f(x),
则f(x)=2[1-(x-3)2](2<x≤4)
作出y=lnx和y=f(x)(0<x<4)的图象,
观察有3个交点,故①对;
对于②,画出y=f(x)(0≤x≤4)
和y=|2x-1|(x<0)的图象,以及直线y=-ax,
当a>0时,-a<0,当直线与y=|2x-1|的图象相切时,只有一个零点,故②错;
对于③,令-2<x<0,则0<x+2<2,
则f(x+2)=1-(x+1)2=2f(x),
则有f(x)=
[1-(x+1)2],
(-2<x<0),画出y=a和y=f(x)在
(-2,4)的图象, 由图象观察,
由图象观察,
得
<a<1时,有4个交点即4个零点,
故③对;
对于④,画出y=f(x)和直线y=ax的图象,通过图象观察,当x>0时,由于f(x)不存在最大值,故不可能有三个交点,故④错.
故答案为:①③
 解:对于①,当2<x≤4时,0<x-2≤2,
解:对于①,当2<x≤4时,0<x-2≤2,f(x-2)=1-(x-3)2=
| 1 |
| 2 |
则f(x)=2[1-(x-3)2](2<x≤4)
作出y=lnx和y=f(x)(0<x<4)的图象,
观察有3个交点,故①对;
对于②,画出y=f(x)(0≤x≤4)
和y=|2x-1|(x<0)的图象,以及直线y=-ax,

当a>0时,-a<0,当直线与y=|2x-1|的图象相切时,只有一个零点,故②错;
对于③,令-2<x<0,则0<x+2<2,
则f(x+2)=1-(x+1)2=2f(x),
则有f(x)=
| 1 |
| 2 |
(-2<x<0),画出y=a和y=f(x)在
(-2,4)的图象,
 由图象观察,
由图象观察,得
| 1 |
| 2 |
故③对;
对于④,画出y=f(x)和直线y=ax的图象,通过图象观察,当x>0时,由于f(x)不存在最大值,故不可能有三个交点,故④错.
故答案为:①③
点评:本题考查函数的零点问题,考查数形结合的思想方法,考查函数方程的转化思想,考查判断能力,属于中档题.

练习册系列答案
相关题目
已知集合M{x|x2-x>0},N={0,1,2,3},则(∁UM)∩N=( )
| A、{x|0≤x≤1} |
| B、{0,1} |
| C、{2,3} |
| D、{1,2,3} |
已知关于x的不等式
-
>0的解集为(-∞,-2)∪(1,2),则关于x的不等式
-
>0的解集为( )
| x+a |
| x+b |
| x+c |
| x+d |
| alnx-1 |
| blnx-1 |
| clnx-1 |
| dlnx-1 |
A、(-1,-
| ||||||||
B、(
| ||||||||
C、(-∞,-
| ||||||||
D、(-∞,
|
已知cos(
+α)=-
,且α为第四象限角,则cos(-3π+α)=( )
| 3π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
下列说法错误的是( )
| A、在统计里,把所需考察对象的全体叫作总体 |
| B、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| C、一组数据的平均数一定大于这组数据中的每个数据 |
| D、一组数据的方差越大,说明这组数据的波动越大 |
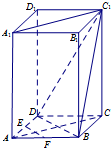 在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.
在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.