题目内容
已知函数f(x)=1-x2,函数g(x)=2ax-3a+2(a>0),若对任意x1∈[0,1],存在x2∈[
,1],使得f(x1)=g(x2)成立,则实数a的值是 .
| 1 |
| 2 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:由任意的x1∈[0,1],都存在x2∈[
,1],使得f(x1)=g(x2),可得f(x)=1-x2在x1∈[0,1]的值域为g(x)=2ax-3a+2在x2∈[
,1]的值域的子集,构造关于a的不等式组,可得结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:当x1∈[0,1]时,由f(x)=1-x2得,
f(x1)∈[0,1],
∵x2∈[
,1],又a>0,
∴g(x2)∈[2-2a,2-a],
∵对任意的x1∈[0,1],都存在x2∈[
,1],使得f(x1)=g(x2),
∴[0,1]⊆[2-2a,2-a],
∴
即
,
∴a=1,
故答案为:1.
f(x1)∈[0,1],
∵x2∈[
| 1 |
| 2 |
∴g(x2)∈[2-2a,2-a],
∵对任意的x1∈[0,1],都存在x2∈[
| 1 |
| 2 |
∴[0,1]⊆[2-2a,2-a],
∴
|
|
∴a=1,
故答案为:1.
点评:本题考查的知识点是二次函数、一次函数在闭区间上的最值问题,其中根据已知条件分析出“f(x)=1-x2在x1∈[0,1]的值域为g(x)=2ax-3a+2在x2∈[
,1]的值域的子集”是解答的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
 如果执行如图所示的框图,输入如下四个复数:
如果执行如图所示的框图,输入如下四个复数:(1)z=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
那么输出的复数是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
执行如图的程序框图输出的T的值为( )


| A、4 | B、6 | C、8 | D、10 |
设
,
是非零向量,则“
-
=
”是“
∥
”的( )
| a |
| b |
| a |
| b |
| 0 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
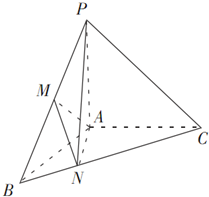 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.