题目内容
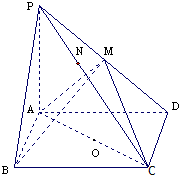 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.(Ⅰ)求证:平面ABM⊥平面PCD;
(Ⅱ)求直线CD与平面ACM所成的角的正弦值;
(Ⅲ)求点N到平面ACM的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)要证平面ABM⊥平面PCD,只需证明平面PCD内的直线PD,垂直平面PAD内的两条相交直线BM、AB即可;
(Ⅱ)先根据体积相等求出D到平面ACM的距离为h,即可求直线PC与平面ABM所成的角;
(Ⅲ)先根据条件分析出所求距离等于点P到平面ACM距离的
,设点P到平面ACM距离为h,再利用第二问的结论即可得到答案.
(Ⅱ)先根据体积相等求出D到平面ACM的距离为h,即可求直线PC与平面ABM所成的角;
(Ⅲ)先根据条件分析出所求距离等于点P到平面ACM距离的
| 5 |
| 9 |
解答:
 (Ⅰ)证明:依题设知,AC是所作球面的直径,
(Ⅰ)证明:依题设知,AC是所作球面的直径,
则AM⊥MC.
又因为P A⊥平面ABCD,则PA⊥CD,又CD⊥AD,
所以CD⊥平面PAD,则CD⊥AM,
所以A M⊥平面PCD,
所以平面ABM⊥平面PCD--------(5分)
(Ⅱ)解:由(Ⅰ)知,AM⊥PD,又PA=AD,则M是PD的中点可得AM=2
,MC=
=2
则S△ACM=
AM•MC=2
,
设D到平面ACM的距离为h,
由VD-ACM=VM-ACD即2
h=8,
可求得h=
,
设所求角为θ,则sinθ=
=
.--------(10分)
(Ⅲ)解:可求得PC=6,因为AN⊥NC,由
=
,得PN=
,
所以NC:PC=5:9,
故N点到平面ACM的距离等于P点到平面ACM距离的
.
又因为M是PD的中点,则P、D到平面ACM的距离相等,
由(Ⅱ)可知所求距离为
h=
.--------(14分)
 (Ⅰ)证明:依题设知,AC是所作球面的直径,
(Ⅰ)证明:依题设知,AC是所作球面的直径,则AM⊥MC.
又因为P A⊥平面ABCD,则PA⊥CD,又CD⊥AD,
所以CD⊥平面PAD,则CD⊥AM,
所以A M⊥平面PCD,
所以平面ABM⊥平面PCD--------(5分)
(Ⅱ)解:由(Ⅰ)知,AM⊥PD,又PA=AD,则M是PD的中点可得AM=2
| 2 |
| MD2+CD2 |
| 3 |
则S△ACM=
| 1 |
| 2 |
| 6 |
设D到平面ACM的距离为h,
由VD-ACM=VM-ACD即2
| 6 |
可求得h=
2
| ||
| 3 |
设所求角为θ,则sinθ=
| h |
| CD |
| ||
| 3 |
(Ⅲ)解:可求得PC=6,因为AN⊥NC,由
| PN |
| PA |
| PA |
| PC |
| 8 |
| 3 |
所以NC:PC=5:9,
故N点到平面ACM的距离等于P点到平面ACM距离的
| 5 |
| 9 |
又因为M是PD的中点,则P、D到平面ACM的距离相等,
由(Ⅱ)可知所求距离为
| 5 |
| 9 |
10
| ||
| 27 |
点评:本题考查直线与平面所成的角,平面与平面垂直的判定,三垂线定理,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知方程
=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是( )
| |sinx| |
| x |
| A、sinα=αcosβ |
| B、sinα=-αcosβ |
| C、cosα=βsinβ |
| D、sinβ=-βsinα |
 如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,D、E、F分别是PC、AC、BC的中点.
如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,D、E、F分别是PC、AC、BC的中点.