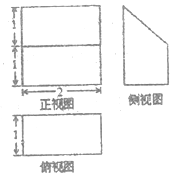
题目内容
15.已知过点M(1,-1)的直线l与椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$相交于A,B两点,若点M是AB的中点,则直线l的方程为3x-4y-7=0.分析 方法一:设直线l的方程,代入椭圆方程,利用中点坐标公式,即可求得直线AB的斜率,利用点斜式方程,即可求得直线l的方程;
方法二:设M(1+m,-1+n),N(1-m,-1-n),代入椭圆方程,作差,由直线l的斜率$\frac{n}{m}$=$\frac{3}{4}$,利用点斜式方程,即可求得直线l的方程.
解答 解:方法一:设A(x1,y1),B(x2,y2),
由中点坐标公式可知:x1+x2=2,y1+y2=-2,
则$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{3}=1}\\{\frac{{x}_{2}^{2}}{4}+\frac{{y}_{2}^{2}}{3}=1}\end{array}\right.$,两式相减得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{4}$+$\frac{{({y}_{1}+{y}_{2})(y}_{1}-{y}_{2})}{3}$=0,
则$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3({x}_{1}+{x}_{2})}{4({y}_{1}+{y}_{2})}$=$\frac{3}{4}$,
则直线AB的斜率k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{3}{4}$,则直线l的方程方程y+1=$\frac{3}{4}$(x-1),
整理得:3x-4y-7=0,
故答案为:3x-4y-7=0.
方法二:由点M是AB的中点,则设M(1+m,-1+n),N(1-m,-1-n),
则$\frac{(1+m)^{2}}{4}+\frac{(-1+n)^{2}}{3}=1$,①
$\frac{(1-m)^{2}}{4}+\frac{(-1-n)}{3}=1$,②
两式相减得:$\frac{2m}{4}+\frac{-2n}{3}=0$,
整理得:$\frac{n}{m}$=$\frac{3}{4}$,
直线AB的斜率k=$\frac{n}{m}$=$\frac{3}{4}$,则直线l的方程方程y+1=$\frac{3}{4}$(x-1),
整理得:3x-4y-7=0,
故答案为:3x-4y-7=0.
点评 本题考查直线与椭圆的位置关系,考查点差法的应用,中点坐标公式,考查计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0 | B. | 1 | C. | 2 | D. | -3 |
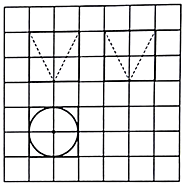 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | $20+\sqrt{5}π$ | B. | $24+\sqrt{5}π$ | C. | $20+(\sqrt{5}-1)π$ | D. | $24+(\sqrt{5}-1)π$ |

| A. | 6+6π | B. | 6+8π | C. | 8+6π | D. | 8+8π |
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |