题目内容
20.设α为△ABC的内角,且tanα=-$\frac{3}{4}$,则cos2α的值为( )| A. | $\frac{7}{25}$ | B. | -$\frac{24}{25}$ | C. | -$\frac{1}{25}$ | D. | $\frac{1}{25}$ |
分析 利用同角三角函数的基本关系,二倍角的余弦公式,求得cos2α的值.
解答 解:∵α为△ABC的内角,且tanα=-$\frac{3}{4}$,则cos2α=$\frac{{cos}^{2}α{-sin}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{{1-tan}^{2}α}{{tan}^{2}α+1}$=$\frac{1-\frac{9}{16}}{\frac{9}{16}+1}$=$\frac{7}{25}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系,二倍角的余弦公式的应用,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.下面四个命题中的真命题是( )
| A. | 命题“?x≥2,均有x2-3x+2≥0”的否定是:“?x<2,使得x2-3x+2<0” | |
| B. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5、16、27、38、49的同学均被选出,则该班人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.3,则X在(0,2)内取值的概率为0.6 |
15.已知函数f(x)的导函数f′(x)的图象如图所示,那么下面说法正确的是( )
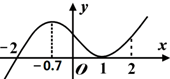

| A. | y=f(x)在(-∞,-0.7)上单调递增 | B. | y=f(x)在(-2,2)上单调递增 | ||
| C. | 在x=1时,函数y=f(x)取得极值 | D. | y=f(x)在x=0处切线的斜率小于零. |
5.与函数f(x)=2x的图象关于直线y=x对称的曲线C对应的函数为g(x),则函数$y=g({\frac{1}{x}})•g({4x})({\frac{1}{8}≤x≤4})$的值域为[-8,1].
9.已知函数f(x)=$\left\{{\begin{array}{l}{{{(\frac{1}{2})}^x}+\frac{3}{4},x≥2}\\{{{log}_2}x,0<x<2}\end{array}}$若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是( )
| A. | 0<k<1 | B. | k>1 | C. | $\frac{3}{4}$<k<1 | D. | k>1或k=$\frac{3}{4}$ |