题目内容
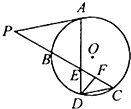 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=考点:与圆有关的比例线段
专题:选作题,立体几何
分析:证明△DEF∽△CED,求出AE,证明△DEF∽△PEA,根据三角形相似得到对应线段成比例,把比例式转化为乘积式,求出EP,再证明EP:EC=AE:ED,求出EC,利用相交弦定理求出EB,即可得出结论.
解答:
解:∵CD∥AP,
∴∠P=∠C,
∵∠EDF=∠P,
∴∠EDF=∠C,
∵∠DEF=∠CED,
∴△DEF∽△CED.
∴DE:CE=EF:ED,
∵EF=4,FC=5,
∴DE=6,
∵AE•ED=BE•EC,
∴AE=12
∵∠P=∠EDF,∠DEF=∠PEA,
∴△DEF∽△PEA.
∴DE:PE=EF:EA.
即EF•EP=DE•EA.
∵AE=12,ED=6,EF=4,
∴4•EP=72,
∴EP=18,
∵CD∥AP,
∴EP:EC=AE:ED,
∴EC=9,
∵弦AD、BC相交于点E,
∴DE•EA=CE•EB,
∴EB=8,
∴PB=EP-EB=10.
故答案为:10.
∴∠P=∠C,
∵∠EDF=∠P,
∴∠EDF=∠C,
∵∠DEF=∠CED,
∴△DEF∽△CED.
∴DE:CE=EF:ED,
∵EF=4,FC=5,
∴DE=6,
∵AE•ED=BE•EC,
∴AE=12
∵∠P=∠EDF,∠DEF=∠PEA,
∴△DEF∽△PEA.
∴DE:PE=EF:EA.
即EF•EP=DE•EA.
∵AE=12,ED=6,EF=4,
∴4•EP=72,
∴EP=18,
∵CD∥AP,
∴EP:EC=AE:ED,
∴EC=9,
∵弦AD、BC相交于点E,
∴DE•EA=CE•EB,
∴EB=8,
∴PB=EP-EB=10.
故答案为:10.
点评:本题考查三角形相似的判断,考查相交弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为X,则P(X≥2)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知定义在R上的可导函数f(x)满足:f′(x)+f(x)<0,则
与f(1)(e是自然对数的底数)的大小关系是( )
| f(m-m2) |
| em2-m+1 |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |