题目内容
某地政府召集6家企业的负责人开会,其中企业甲有3人到会,企业乙有2人到会,其余4家企业各有一人到会,会上有3人发言,则这3人来自3家不同企业的情况种数为 .
考点:计数原理的应用
专题:排列组合
分析:本题是一个分类计数问题,分四类,无甲无乙,有甲无乙,无甲有乙,有甲有乙,根据分类计数原理得到结果.
解答:
解:由题意知本题是一个分类计数问题,
第一类,无甲无乙,选法有
=4种,
第二类,有甲无乙,选法有
=18种,
第三类,无甲有乙,选法有C21C42=12种,
第四类,有甲有乙,选法有
=24种,
这3人来自3家不同企业的情况共有4+18+12+24=58种.
故答案为:58.
第一类,无甲无乙,选法有
| C | 3 4 |
第二类,有甲无乙,选法有
| C | 1 3 |
| •C | 2 4 |
第三类,无甲有乙,选法有C21C42=12种,
第四类,有甲有乙,选法有
| C | 1 3 |
| •C | 1 2 |
| •C | 1 4 |
这3人来自3家不同企业的情况共有4+18+12+24=58种.
故答案为:58.
点评:本题考查分类计数问题,在排列的过程中出现有特殊情况的元素,需要分类来解,不然不能保证发言的3人来自3家不同企业.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设复数z=(1-2i)(a+i)(a∈R)在复平面内对应的点为M,则“a>
”是“点M在第四象限”的什么条件
( )
| 2 |
| 5 |
( )
| A、充分不必要 |
| B、必要不充分 |
| C、充分且必要 |
| D、既不充分也不必要 |
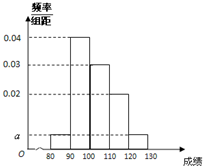 为了分析我校市二模文科数学的成绩,现抽样统计了20位同学的数学成绩,形成了如图所示的频率分布直方图,其中成绩的分组区间是:[80,90),[90,100),[100,110),[110,120),[120,130]
为了分析我校市二模文科数学的成绩,现抽样统计了20位同学的数学成绩,形成了如图所示的频率分布直方图,其中成绩的分组区间是:[80,90),[90,100),[100,110),[110,120),[120,130]