题目内容
已知f(x)=2sin(x-
)cos(x-
)+2
cos2(x-
)
(Ⅰ)求f(x)的最大值及取到最大值时相应的x的集合;
(Ⅱ)若函数y=f(x)=-m在区间[0,
]上恰好有两个零点,求实数m的取值范围.
| π |
| 4 |
| π |
| 4 |
| 3 |
| π |
| 4 |
(Ⅰ)求f(x)的最大值及取到最大值时相应的x的集合;
(Ⅱ)若函数y=f(x)=-m在区间[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)先对函数解析式进行化简,进而根据三角函数的性质求得函数的最大值及此时x的范围.
(Ⅱ)根据x的范围,画出f(x)的图象,利用数形结合方法求得答案.
(Ⅱ)根据x的范围,画出f(x)的图象,利用数形结合方法求得答案.
解答:
解:(Ⅰ)f(x)=2sin(x-
)cos(x-
)+2
cos2(x-
)
=sin(2x-
)+
cos(2x-
)+
=2sin(2x-
)+
∴函数的最大值为2+
,
当2x-
=2kπ+
(k∈Z),即x=kπ+
(k∈Z)时取最大值,
∴取到最大值时相应的x的集合为{x|x=kπ+
,(k∈Z)}
(Ⅱ)依(Ⅰ)知f(x)=2sin(2x-
)+
当x∈[0,
]时,2x-
∈[-
,
],
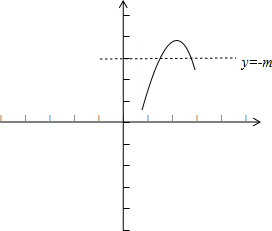
要使函数y=f(x)=-m有两个零点即直线与函数的图象有两个交点,依草图可知f(
)≤-m<f(x)max
即-1-
≥m>-2-
.
| π |
| 4 |
| π |
| 4 |
| 3 |
| π |
| 4 |
=sin(2x-
| π |
| 2 |
| 3 |
| π |
| 2 |
| 3 |
=2sin(2x-
| π |
| 6 |
| 3 |
∴函数的最大值为2+
| 3 |
当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴取到最大值时相应的x的集合为{x|x=kπ+
| π |
| 3 |
(Ⅱ)依(Ⅰ)知f(x)=2sin(2x-
| π |
| 6 |
| 3 |
当x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
要使函数y=f(x)=-m有两个零点即直线与函数的图象有两个交点,依草图可知f(
| π |
| 2 |
即-1-
| 3 |
| 3 |

点评:本题主要考查了三角函数恒等变换的应用.注意对数形结合思想的灵活运用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目