题目内容
15.已知tanx=$\frac{4}{3}$(π<x<$\frac{3}{2}$π),则cos(2x-$\frac{π}{3}$)cos($\frac{π}{3}$-x)-sin(2x-$\frac{π}{3}$)•sin($\frac{π}{3}$-x)=-$\frac{3}{5}$.分析 由条件利用同角三角函数的基本关系求得cosx的值,再利用两角和差的余弦公式化简要求的式子,可得结果.
解答 解:∵tanx=$\frac{4}{3}$=$\frac{sinx}{cosx}$ (π<x<$\frac{3}{2}$π),sin2x+cos2x=1,sinx<0,cosx<0,
∴sinx=-$\frac{4}{5}$,cosx=-$\frac{3}{5}$,
则cos(2x-$\frac{π}{3}$)cos($\frac{π}{3}$-x)-sin(2x-$\frac{π}{3}$)•sin($\frac{π}{3}$-x)=cos(2x-$\frac{π}{3}$+$\frac{π}{3}$-x)
=cosx=-$\frac{3}{5}$,
故答案为:-$\frac{3}{5}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
5.已知函数f(x)=cos2x+asinx在区间(0,nπ)内恰有8个零点,则实数a的取值范围与最小正整数n的值分别为( )
| A. | (-1,1),2 | B. | (-1,1),4 | C. | [-1,1],2 | D. | [-1,1],4 |
3.已知集合M={x|0<x<2},N={x|x>1},则M∩N=( )
| A. | [1,2) | B. | (1,2) | C. | [0,1) | D. | (0,1] |
20.(x2-x+1)3展开式中x项的系数为( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
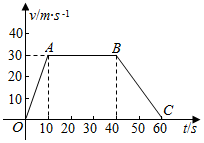 一辆汽车的速度一时间曲线如图所示,求汽车在这1min内行驶的路程.
一辆汽车的速度一时间曲线如图所示,求汽车在这1min内行驶的路程.